A student
A student is to answer 8 out of 10 questions on the exam.
a) find the number n of ways the student can choose 8 out of 10 questions
b) find n if the student must answer the first three questions
c) How many if he must answer at least 4 of the first five questions?
a) find the number n of ways the student can choose 8 out of 10 questions
b) find n if the student must answer the first three questions
c) How many if he must answer at least 4 of the first five questions?
Correct answer:

Tips for related online calculators
Would you like to compute the count of combinations?
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Defect rate
 A manufacturing machine has a 3% defect rate. If 9 items are chosen randomly, what is the probability that at least one will have a defect?
A manufacturing machine has a 3% defect rate. If 9 items are chosen randomly, what is the probability that at least one will have a defect? - A basket 4
 A basket contains 9 fruits, where 4 are oranges, and the rest are mangoes. Three fruits are taken out one at a time and put aside. Find the probability that 3 are oranges.
A basket contains 9 fruits, where 4 are oranges, and the rest are mangoes. Three fruits are taken out one at a time and put aside. Find the probability that 3 are oranges. - A ferry
 A ferry with a capacity of 10 people takes a group of 13 men and 7 women across a river. Find the number of ways in which the group may be taken across the if all women go on the first group.
A ferry with a capacity of 10 people takes a group of 13 men and 7 women across a river. Find the number of ways in which the group may be taken across the if all women go on the first group. - Two dice 3
 Two dice are thrown together. What is the probability that the number obtained on one of the dice is a multiple of the number obtained on the other dice? 2/3 9/36 12/36 11/18
Two dice are thrown together. What is the probability that the number obtained on one of the dice is a multiple of the number obtained on the other dice? 2/3 9/36 12/36 11/18 - Student examination
 How many ways can a teacher select a group of 6 students to sit in the front row if the class has 13 students?
How many ways can a teacher select a group of 6 students to sit in the front row if the class has 13 students? - How many 31
 How many ways can a teacher select a group of 3 students to sit in the front row if the class has 13 students?
How many ways can a teacher select a group of 3 students to sit in the front row if the class has 13 students? - 52 cards
 A hand of five cards is dealt from a pack of 52 playing cards. How many different hands can be dealt that contain three aces?
A hand of five cards is dealt from a pack of 52 playing cards. How many different hands can be dealt that contain three aces? - A disease
 A disease affects 10% of the individuals in a population, and a sample of 100 people was selected from the population. What is the probability of finding the disease in at least 15 people?
A disease affects 10% of the individuals in a population, and a sample of 100 people was selected from the population. What is the probability of finding the disease in at least 15 people? - Manufacturing company
 It is established by the production manager of a manufacturing company that 2 out of every 20 units of a particular product are faulty. In a particular production hour, 8 units of the product were produced. Determine the probability that: (1) none of them
It is established by the production manager of a manufacturing company that 2 out of every 20 units of a particular product are faulty. In a particular production hour, 8 units of the product were produced. Determine the probability that: (1) none of them - Containers
 One in eight containers is temporarily misplaced. A random sample of 12 containers is selected. What is the probability that 6 of these containers will be temporarily misplaced?
One in eight containers is temporarily misplaced. A random sample of 12 containers is selected. What is the probability that 6 of these containers will be temporarily misplaced? - The triangle 5
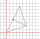 The triangle below has vertices A(-1,-2), B(2,2), and C(-1,4). What is the area of △ABCin square coordinate units?
The triangle below has vertices A(-1,-2), B(2,2), and C(-1,4). What is the area of △ABCin square coordinate units? - The chief
 The chief fisherman Peter estimates that if he uses four lines, then the probability of making a catch on one line is 0.7. If he uses five lines, then the probability of making a catch on any line is 0.6. If he uses six lines, the probability of making a
The chief fisherman Peter estimates that if he uses four lines, then the probability of making a catch on one line is 0.7. If he uses five lines, then the probability of making a catch on any line is 0.6. If he uses six lines, the probability of making a - Yarhands
 Yarhands statistical consult conducted statistical analysis on the election results from 1992 to 2012 to assess the chances of the NPP winning the election in Ghana's Volta region. The research reveals that 15% of inhabitants in the Volta region favor the
Yarhands statistical consult conducted statistical analysis on the election results from 1992 to 2012 to assess the chances of the NPP winning the election in Ghana's Volta region. The research reveals that 15% of inhabitants in the Volta region favor the - Bernoulli trial
 A used car saleswoman estimates that each time she shows a customer a car, there is a probability of 0.1 that the customer will buy the car. The saleswoman would like to sell at least one car per week. If showing a car is a Bernoulli trial with a probabil
A used car saleswoman estimates that each time she shows a customer a car, there is a probability of 0.1 that the customer will buy the car. The saleswoman would like to sell at least one car per week. If showing a car is a Bernoulli trial with a probabil - A committee
 A committee of 6 is chosen from 8 men and seven women. Find how many committees are possible if a particular man must be included.
A committee of 6 is chosen from 8 men and seven women. Find how many committees are possible if a particular man must be included. - A bag 2
 A bag contains seven green and eight red jellybeans. How many ways can five jellybeans be withdrawn from the bag so that the number of green ones withdrawn will be less than 4?
A bag contains seven green and eight red jellybeans. How many ways can five jellybeans be withdrawn from the bag so that the number of green ones withdrawn will be less than 4? - Competition 73174
 There are 10 students in the class, of which 8 are girls and two are boys. We want to select three for the competition. What is the probability that they will be: a) 2 girls and 1 boy b) 1 girl and 2 boys c) 3 girls d) 3 boys e) at least 2 girls
There are 10 students in the class, of which 8 are girls and two are boys. We want to select three for the competition. What is the probability that they will be: a) 2 girls and 1 boy b) 1 girl and 2 boys c) 3 girls d) 3 boys e) at least 2 girls
