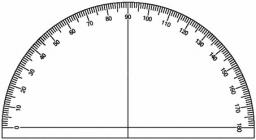
Reference angle
Find the reference angle of each angle:
Correct answer:
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Six-sided polygon
 There is a six-sided polygon. The first two angles are equal, the third angle is twice (the equal angles), two other angles are trice the equal angle, while the last angle is a right angle. Find the value of each angle.
There is a six-sided polygon. The first two angles are equal, the third angle is twice (the equal angles), two other angles are trice the equal angle, while the last angle is a right angle. Find the value of each angle. - Right angle
 If a, b and c are two sides of a triangle ABC, a right angle in A, find the value on each missing side. If b=10, c=6
If a, b and c are two sides of a triangle ABC, a right angle in A, find the value on each missing side. If b=10, c=6 - The angles 4
 The angles of a triangle are divided into the ratio 126: 213: 312. If the three angles sum to 180°, find the size of each of the three angles.
The angles of a triangle are divided into the ratio 126: 213: 312. If the three angles sum to 180°, find the size of each of the three angles. - In a 2
 In a thirteen-sided polygon, the sum of five angles is 1274°, four of the eight angles remaining are equal, and the other four are 18° less than each of the equal angles. Find the angles.
In a thirteen-sided polygon, the sum of five angles is 1274°, four of the eight angles remaining are equal, and the other four are 18° less than each of the equal angles. Find the angles. - Area of iso-trap
 Find the area of an isosceles trapezoid if the lengths of its bases are 16 cm and 30 cm, and the diagonals are perpendicular to each other.
Find the area of an isosceles trapezoid if the lengths of its bases are 16 cm and 30 cm, and the diagonals are perpendicular to each other. - A Cartesian framework
 1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap
1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap - Perpendicular and parallel
 Find the value of t if 2tx+5y-6=0 and 5x-4y+8=0 are perpendicular and parallel lines. What angle does each line make with the x-axis, and find the angle between the lines?
Find the value of t if 2tx+5y-6=0 and 5x-4y+8=0 are perpendicular and parallel lines. What angle does each line make with the x-axis, and find the angle between the lines? - Circumference 7143
 Peter drew a regular hexagon, the vertices of which lay on a circle 16 cm long. Then, for each vertex of this hexagon, he drew a circle centered on that vertex that ran through its two adjacent vertices. The unit was created as in the picture. Find the ci
Peter drew a regular hexagon, the vertices of which lay on a circle 16 cm long. Then, for each vertex of this hexagon, he drew a circle centered on that vertex that ran through its two adjacent vertices. The unit was created as in the picture. Find the ci - A rhombus 4
 A rhombus has a side length of 10 cm. Find the angles at each corner of the rhombus if the shorter of the two diagonals measures 7 cm. Give your answers to the nearest degree and give clear geometric reasoning at each stage of your solution.
A rhombus has a side length of 10 cm. Find the angles at each corner of the rhombus if the shorter of the two diagonals measures 7 cm. Give your answers to the nearest degree and give clear geometric reasoning at each stage of your solution. - Trapezoid MO
 The rectangular trapezoid ABCD with the right angle at point B, |AC| = 12, |CD| = 8, diagonals are perpendicular to each other. Calculate the perimeter and area of the trapezoid.
The rectangular trapezoid ABCD with the right angle at point B, |AC| = 12, |CD| = 8, diagonals are perpendicular to each other. Calculate the perimeter and area of the trapezoid. - Perpendicular 7223
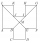 In the ABCDEFGHIJKL, the two adjacent sides are perpendicular to each other, and all sides except the AL and GF sides are identical. The AL and GF parties are twice as long as the other parties. The lines BG and EL intersect at point M. The quadrilateral
In the ABCDEFGHIJKL, the two adjacent sides are perpendicular to each other, and all sides except the AL and GF sides are identical. The AL and GF parties are twice as long as the other parties. The lines BG and EL intersect at point M. The quadrilateral - Determine 4314
 Find the rank of each null matrix.
Find the rank of each null matrix. - Modulus and argument
 Find the mod z and argument z if z=i
Find the mod z and argument z if z=i - Minute angle
 Find the size of the angle, which takes a minute hand for 20 minutes.
Find the size of the angle, which takes a minute hand for 20 minutes. - Slope
 Find the slope of the line: x=t and y=1+t.
Find the slope of the line: x=t and y=1+t. - Trapezoid - RR
 Find the area of the right-angled trapezoid ABCD with the right angle at the A vertex; a = 3 dm b = 5 dm c = 6 dm d = 4 dm
Find the area of the right-angled trapezoid ABCD with the right angle at the A vertex; a = 3 dm b = 5 dm c = 6 dm d = 4 dm - Nonagon
 Calculate the area and perimeter of a regular nonagon if its radius of the inscribed circle is r = 10cm
Calculate the area and perimeter of a regular nonagon if its radius of the inscribed circle is r = 10cm
