Practice
How many ways can you place 20 pupils in a row when starting on practice?
Correct answer:

Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Starting 38113
 How many ways can we put 19 students in a row when starting a gym?
How many ways can we put 19 students in a row when starting a gym? - Friends in cinema
 5 friends went to the cinema. How many possible ways can they sit in a row if one of them wants to sit in the middle and the remaining place does not matter?
5 friends went to the cinema. How many possible ways can they sit in a row if one of them wants to sit in the middle and the remaining place does not matter? - Guests
 How many ways can 8 guests sit down on 10 seats standing in a row?
How many ways can 8 guests sit down on 10 seats standing in a row? - Participants 8335
 How many ways can you be rewarded in the 1st, 2nd, or 3rd place? The prize for 15 participants in the competition?
How many ways can you be rewarded in the 1st, 2nd, or 3rd place? The prize for 15 participants in the competition? - Different 42371
 How many ways can you store seven different books side-by-side when a math book has to be on the edge of the shelf?
How many ways can you store seven different books side-by-side when a math book has to be on the edge of the shelf? - School group
 There are five girls and seven boys in the group. They sit in a row next to each other. How many options if no two girls sit next to each other?
There are five girls and seven boys in the group. They sit in a row next to each other. How many options if no two girls sit next to each other? - Five couples
 In how many ways can 5 couples arrange themselves in a row if they stay together?
In how many ways can 5 couples arrange themselves in a row if they stay together? - Chessboard 80533
 How many ways can one white and one black square be selected on an 8x8 chessboard if the selected squares cannot lie in the same row or column?
How many ways can one white and one black square be selected on an 8x8 chessboard if the selected squares cannot lie in the same row or column? - How many 31
 How many ways can a teacher select a group of 3 students to sit in the front row if the class has 13 students?
How many ways can a teacher select a group of 3 students to sit in the front row if the class has 13 students? - Motion
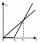 The two bodies move in the same direction evenly in a straight line, at speeds of 5 cm/s and 10 cm/s. The movement of the first body started 2 seconds earlier than the movement of the second body, from a point located at a distance of 20 cm from the start
The two bodies move in the same direction evenly in a straight line, at speeds of 5 cm/s and 10 cm/s. The movement of the first body started 2 seconds earlier than the movement of the second body, from a point located at a distance of 20 cm from the start - Doesn't 37531
 How many ways can you draw eight playing cards from 32 playing cards when their order doesn't matter?
How many ways can you draw eight playing cards from 32 playing cards when their order doesn't matter? - Bookshelf and books
 How many ways can we place seven books on a bookshelf?
How many ways can we place seven books on a bookshelf? - Football 5788
 Tomas has four football jerseys: red, blue, white, and green. How many ways can Tomáš place them on the shelf next to each other so that the red and blue jerseys are adjacent?
Tomas has four football jerseys: red, blue, white, and green. How many ways can Tomáš place them on the shelf next to each other so that the red and blue jerseys are adjacent? - Cups on the shelf
 We should place two green, three red, and two yellow cups side by side on the shelf. a) How many different ways of setting up can arise? b) How many different ways of arranging can arise if cups of the same color stand side by side?
We should place two green, three red, and two yellow cups side by side on the shelf. a) How many different ways of setting up can arise? b) How many different ways of arranging can arise if cups of the same color stand side by side? - Football league
 In the 5th football league is 10 teams. How many ways can be filled first, second, and third place?
In the 5th football league is 10 teams. How many ways can be filled first, second, and third place? - Checkerboard 9091
 Determine how many ways we can place 5 different pieces on an 8x8 chessboard so that two are on black squares and three are on white squares?
Determine how many ways we can place 5 different pieces on an 8x8 chessboard so that two are on black squares and three are on white squares? - Covid-19 spread
 A Street has 13 houses in a row. Some residents in the first house tested positive for Covid-19. The virus spreads in 2 ways: It can spread to the next house or jump directly to the third house. Residents of house two can get infected in only one way, hou
A Street has 13 houses in a row. Some residents in the first house tested positive for Covid-19. The virus spreads in 2 ways: It can spread to the next house or jump directly to the third house. Residents of house two can get infected in only one way, hou
