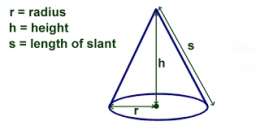
The diagram 2
The diagram shows a cone with a slant height of 10.5cm. If the curved surface area of the cone is 115.5 cm2. Calculate to correct three significant figures:
*Base Radius
*Height
*Volume of the cone
*Base Radius
*Height
*Volume of the cone
Correct answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- solid geometry
- cone
- planimetrics
- Pythagorean theorem
- right triangle
- circle
- triangle
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- A cone 2
 A cone has a slant height of 10 cm and a square curved surface area of 50 pi cm. Find the base radius of the cone.
A cone has a slant height of 10 cm and a square curved surface area of 50 pi cm. Find the base radius of the cone. - The diagram
 The diagram shows a cone radius of 8cm and a height of 10cm. How long is the diameter of the base?
The diagram shows a cone radius of 8cm and a height of 10cm. How long is the diameter of the base? - The base 2
 The base diameter of a right cone is 16cm, and its slant height is 12cm. A. ) Find the perpendicular height of the cone to 1 decimal place. B. ) Find the volume of the cone, and convert it to 3 significant figures. Take pi =3.14
The base diameter of a right cone is 16cm, and its slant height is 12cm. A. ) Find the perpendicular height of the cone to 1 decimal place. B. ) Find the volume of the cone, and convert it to 3 significant figures. Take pi =3.14 - Rotating 6245
 How does the volume of the rotating cone change if: a) double the radius of the base b) We reduce the height three times c) Reduce the radius of the base five times
How does the volume of the rotating cone change if: a) double the radius of the base b) We reduce the height three times c) Reduce the radius of the base five times
- The radius
 A right circular cone's radius and slant heights are 9 cm and 15 cm, respectively. Find, correct to one decimal place, the (i) Height (ii) Volume of the cone
A right circular cone's radius and slant heights are 9 cm and 15 cm, respectively. Find, correct to one decimal place, the (i) Height (ii) Volume of the cone - Slant height
 The cone's slant height is 5cm, and the radius of its base is 3cm, so find the cone's volume.
The cone's slant height is 5cm, and the radius of its base is 3cm, so find the cone's volume. - Rotating cone II
 Calculate the area of the surface of a rotating cone with base radius r=15 cm and height h=13 cm.
Calculate the area of the surface of a rotating cone with base radius r=15 cm and height h=13 cm. - Curved surface area CSA
 A cylinder 5cm high has a base radius(7/2) cm. Calculate the curved surface area.
A cylinder 5cm high has a base radius(7/2) cm. Calculate the curved surface area. - Cone 15
 The radius of the base of a right circular cone is 14 inches, and its height is 18 inches. What is the slant height?
The radius of the base of a right circular cone is 14 inches, and its height is 18 inches. What is the slant height?
- A sphere
 A sphere has a radius of 5.5 cm. Determine its volume and surface area. A frustum of the sphere is formed by two parallel planes. One through the diameter of the curved surface of the frustum is to be of the surface area of the sphere. Find the height and
A sphere has a radius of 5.5 cm. Determine its volume and surface area. A frustum of the sphere is formed by two parallel planes. One through the diameter of the curved surface of the frustum is to be of the surface area of the sphere. Find the height and - Calculate 5789
 Calculate the volume and surface of the rotating cone with the base radius r = 4.6dm and the height v = 230mm.
Calculate the volume and surface of the rotating cone with the base radius r = 4.6dm and the height v = 230mm. - Parameters 28521
 The basic parameters of the rotating cone are: Base radius 5 cm Cone height 12 cm and cone side 13 cm. Calculate: a/volume of the cone b/cone surface
The basic parameters of the rotating cone are: Base radius 5 cm Cone height 12 cm and cone side 13 cm. Calculate: a/volume of the cone b/cone surface - Frustrum - volume, area
 Calculate the surface and volume of a truncated rotating cone with base radii of 8 cm and 4 cm and a height of 5 cm.
Calculate the surface and volume of a truncated rotating cone with base radii of 8 cm and 4 cm and a height of 5 cm. - Sphere
 Intersect between the plane and a sphere is a circle with a radius of 60 mm. The cone, whose base is this circle and whose apex is at the center of the sphere, has a height of 34 mm. Calculate the surface area and volume of a sphere.
Intersect between the plane and a sphere is a circle with a radius of 60 mm. The cone, whose base is this circle and whose apex is at the center of the sphere, has a height of 34 mm. Calculate the surface area and volume of a sphere.
- Rotating cone
 Calculate the volume of a rotating cone with base radius r=$r cm and height h=$v cm.
Calculate the volume of a rotating cone with base radius r=$r cm and height h=$v cm. - Calculate 24011
 There is a cylinder with a base radius of 3 cm and a height of 12 cm. Calculate a) cylinder surface b) cylinder volume
There is a cylinder with a base radius of 3 cm and a height of 12 cm. Calculate a) cylinder surface b) cylinder volume - Calculate 24941
 Calculate the surface and volume of a cylinder with a base radius of 5 cm and a height of 8 cm.
Calculate the surface and volume of a cylinder with a base radius of 5 cm and a height of 8 cm.
