Euklid4
The legs of a right triangle have dimensions 244 m and 246 m. Calculate the length of the hypotenuse and the height of this right triangle.
Correct answer:

Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Catheti
 The hypotenuse of a right triangle is 41, and the sum of legs is 49. Calculate the length of its legs.
The hypotenuse of a right triangle is 41, and the sum of legs is 49. Calculate the length of its legs. - Triangular 6950
 A triangular prism has the base of a right triangle with 6 dm and 8 dm legs and a hypotenuse of 10 dm. The height of the prism is 40 dm. What is the volume of a prism?
A triangular prism has the base of a right triangle with 6 dm and 8 dm legs and a hypotenuse of 10 dm. The height of the prism is 40 dm. What is the volume of a prism? - Difference of legs
 In a right triangle, the hypotenuse length is 65 m, and the difference between legs is 23 m. Calculate the perimeter of this triangle.
In a right triangle, the hypotenuse length is 65 m, and the difference between legs is 23 m. Calculate the perimeter of this triangle. - Perpendicular prism
 Calculate the volume of the vertical prism if its height is 60.8 cm and the base is a rectangular triangle with 40.4 cm and 43 cm legs.
Calculate the volume of the vertical prism if its height is 60.8 cm and the base is a rectangular triangle with 40.4 cm and 43 cm legs.
- Hypotenuse and height
 In a right triangle is length of the hypotenuse c = 56 cm and height hc = 4 cm. Determine the length of both triangle legs.
In a right triangle is length of the hypotenuse c = 56 cm and height hc = 4 cm. Determine the length of both triangle legs. - Thales
 Calculate the length of the Thales' circle described to the right triangle with hypotenuse 44.2 cm.
Calculate the length of the Thales' circle described to the right triangle with hypotenuse 44.2 cm. - Right triangle
 Right triangle legs have lengths 630 mm and 411 dm. Calculate the area of this triangle.
Right triangle legs have lengths 630 mm and 411 dm. Calculate the area of this triangle. - Right triangle ABC
 Calculate the perimeter and area of a right triangle ABC. If you know the length of the legs, 4 cm, 5.5 cm, and 6.8 cm are the hypotenuse.
Calculate the perimeter and area of a right triangle ABC. If you know the length of the legs, 4 cm, 5.5 cm, and 6.8 cm are the hypotenuse. - Median in right triangle
 In the rectangular triangle, ABC has known the length of the legs a = 15cm and b = 36cm. Calculate the length of the median to side c (to hypotenuse).
In the rectangular triangle, ABC has known the length of the legs a = 15cm and b = 36cm. Calculate the length of the median to side c (to hypotenuse).
- Hypotenuse
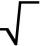 Calculate the length of the hypotenuse of a right triangle with a catheti 71 cm and 49 cm long.
Calculate the length of the hypotenuse of a right triangle with a catheti 71 cm and 49 cm long. - Area of RT
 The right triangle has orthogonal projections of legs to the hypotenuse lengths 15 cm and 9 cm. Determine the area of this triangle.
The right triangle has orthogonal projections of legs to the hypotenuse lengths 15 cm and 9 cm. Determine the area of this triangle. - Hypotenuse 72524
 We know the height of the hypotenuse h = 4cm and the hypotenuse c = 19cm in a right triangle. How to calculate the segments of legs - sections on the hypotenuse c1, c2
We know the height of the hypotenuse h = 4cm and the hypotenuse c = 19cm in a right triangle. How to calculate the segments of legs - sections on the hypotenuse c1, c2 - Perpendicular 32733
 Calculate the right triangle ABC, the perpendicular b = 43.5 cm of the hypotenuse c = 72.9 cm. Calculate: A hypotenuse segment cb, side a, a hypotenuse segment ca, and a height of triangle v
Calculate the right triangle ABC, the perpendicular b = 43.5 cm of the hypotenuse c = 72.9 cm. Calculate: A hypotenuse segment cb, side a, a hypotenuse segment ca, and a height of triangle v - Area of RT 2
 Calculate the area of a right triangle whose legs have a length of 6.2 cm and 9.8 cm.
Calculate the area of a right triangle whose legs have a length of 6.2 cm and 9.8 cm.
- IS triangle
 Calculate interior angles of the isosceles triangle with base 40 cm and legs 22 cm long.
Calculate interior angles of the isosceles triangle with base 40 cm and legs 22 cm long. - RTriangle 17
 The hypotenuse of a right triangle is 17 cm. If you decrease both two legs by 3 cm, you will reduce the hypotenuse by 4 cm. Determine the length of these legs.
The hypotenuse of a right triangle is 17 cm. If you decrease both two legs by 3 cm, you will reduce the hypotenuse by 4 cm. Determine the length of these legs. - Right triangle
 The legs of the right triangle are in the ratio a:b = 2:8. The hypotenuse has a length of 87 cm. Calculate the perimeter and area of the triangle.
The legs of the right triangle are in the ratio a:b = 2:8. The hypotenuse has a length of 87 cm. Calculate the perimeter and area of the triangle.
