Unit conversion + similarity of triangles - practice problems
Number of problems found: 20
- Scale model
 In a model train set, 1.38 inches represents one foot in real life. The height of One World Trade Center in New York City is 1776 feet. How tall would a scale model of the building be? Should you calculate 1776 x 1.38 or 1776 ÷ 1.38?
In a model train set, 1.38 inches represents one foot in real life. The height of One World Trade Center in New York City is 1776 feet. How tall would a scale model of the building be? Should you calculate 1776 x 1.38 or 1776 ÷ 1.38? - Triangle-shaped 30011
 Determine the map's scale if the 1.6 km, 2.4 km, and 2.7 km triangle-shaped forests are drawn on the map as a triangle with sides of 32 mm, 48 mm, and 54 mm.
Determine the map's scale if the 1.6 km, 2.4 km, and 2.7 km triangle-shaped forests are drawn on the map as a triangle with sides of 32 mm, 48 mm, and 54 mm. - Similarity 80742
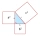 Calculate the perimeter of triangle ABC if you know that it is similar to triangle EFG in which e=144 mm, f=164 mm, g=92 mm, and the similarity ratio is 4. Express the result in cm.
Calculate the perimeter of triangle ABC if you know that it is similar to triangle EFG in which e=144 mm, f=164 mm, g=92 mm, and the similarity ratio is 4. Express the result in cm. - Vertical rod
 The vertical one-meter-long rod casts a shadow 150 cm long. Calculate the height of a column whose shadow is 36 m long simultaneously.
The vertical one-meter-long rod casts a shadow 150 cm long. Calculate the height of a column whose shadow is 36 m long simultaneously. - Chimney and tree
 Calculate the height of the factory chimney, which casts a shadow of 6.5 m long in the afternoon. At the same time, a 6 m high tree standing near it casts a shadow 25 dm long.
Calculate the height of the factory chimney, which casts a shadow of 6.5 m long in the afternoon. At the same time, a 6 m high tree standing near it casts a shadow 25 dm long. - Determine 82470
 The school building casts a shadow 16 m long on the plane of the yard, and at the same time, a vertical meter pole casts a shadow 132 cm long. Determine the height of the building.
The school building casts a shadow 16 m long on the plane of the yard, and at the same time, a vertical meter pole casts a shadow 132 cm long. Determine the height of the building. - Triangle 28611
 The land has a triangle shape with sides of 300m, 200m, and 245m. Draw it on a scale of 1:5 000.
The land has a triangle shape with sides of 300m, 200m, and 245m. Draw it on a scale of 1:5 000. - Similarity 26441
 How long a shadow casts a building 15 m high if the shadow of a meter rod is 90 cm? Sketch - similarity.
How long a shadow casts a building 15 m high if the shadow of a meter rod is 90 cm? Sketch - similarity. - Calculate 64444
 The length of the linden shadow is 429 cm. The length of the shadow meter is 78cm. Calculate the height of the linden.
The length of the linden shadow is 429 cm. The length of the shadow meter is 78cm. Calculate the height of the linden. - The straight
 The straight path rises by 72 cm every 3 m of its length. How many meters will it climb to 350 m?
The straight path rises by 72 cm every 3 m of its length. How many meters will it climb to 350 m? - Shadow of tree
 Miro stands under a tree and watches its shadow and shadow of the tree. Miro is 180 cm tall, and its shade is 1.5 m long. The tree's shadow is three times as long as Miro's shadow. How tall is the tree in meters?
Miro stands under a tree and watches its shadow and shadow of the tree. Miro is 180 cm tall, and its shade is 1.5 m long. The tree's shadow is three times as long as Miro's shadow. How tall is the tree in meters? - Mirror
 How far must Paul place a mirror to see the top of the tower 12 m high? The height of Paul's eyes above the horizontal plane is 160 cm, and Paul is from the tower distance of 20 m.
How far must Paul place a mirror to see the top of the tower 12 m high? The height of Paul's eyes above the horizontal plane is 160 cm, and Paul is from the tower distance of 20 m. - Mast angles and height
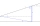 Calculate the height of the mast, whose foot can be seen at a depth angle of 11° and the top at a height angle of 28°. The mast is observed from a position 10 m above the level of the base of the mast.
Calculate the height of the mast, whose foot can be seen at a depth angle of 11° and the top at a height angle of 28°. The mast is observed from a position 10 m above the level of the base of the mast. - Thales
 Thales is 1 m from the hole. The eyes are 150 cm above the ground and look into the hole with a diameter of 120 cm, as shown. Calculate the depth of the hole.
Thales is 1 m from the hole. The eyes are 150 cm above the ground and look into the hole with a diameter of 120 cm, as shown. Calculate the depth of the hole. - Observation 82811
 From the 40 m high observation deck, you can see the top of the poplar at a depth angle of 50*10' and the bottom of the poplar at a depth angle of 58*. Calculate the height of the poplar.
From the 40 m high observation deck, you can see the top of the poplar at a depth angle of 50*10' and the bottom of the poplar at a depth angle of 58*. Calculate the height of the poplar. - Inclined plane
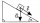 The body stays on an inclined plane and exerts a compressive force of 70N on it. Find the angle between the inclined plane and the horizontal if a gravitational force of 100N acts on the body.
The body stays on an inclined plane and exerts a compressive force of 70N on it. Find the angle between the inclined plane and the horizontal if a gravitational force of 100N acts on the body. - Tree shadow
 The tree perpendicular to the horizontal surface has a shadow 8.32 meters long. At the same time, a one-meter rod perpendicular to the horizontal surface has a shadow 64 cm long. How tall is the tree?
The tree perpendicular to the horizontal surface has a shadow 8.32 meters long. At the same time, a one-meter rod perpendicular to the horizontal surface has a shadow 64 cm long. How tall is the tree? - The chimney
 The chimney casts a shadow 45 meters long. The one-meter-long rod standing perpendicular to the ground has a shadow 90 cm long. Calculate the height of the chimney.
The chimney casts a shadow 45 meters long. The one-meter-long rod standing perpendicular to the ground has a shadow 90 cm long. Calculate the height of the chimney. - Ruler
 Peter is looking at John over a ruler that keeps at an arm's distance of 60 cm from the eye, and on the ruler, John measured the height of 15 mm. John is 2 meters high. How far from Peter stands John?
Peter is looking at John over a ruler that keeps at an arm's distance of 60 cm from the eye, and on the ruler, John measured the height of 15 mm. John is 2 meters high. How far from Peter stands John? - TV diagonal
 A diagonal TV is 0.56 m long. How big the television screen is if the aspect ratio is 16:9?
A diagonal TV is 0.56 m long. How big the television screen is if the aspect ratio is 16:9?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
