Practice problems of the area of a shape - page 7 of 107
The area is the quantity that expresses the extent of a two-dimensional shape. The area can be understood as the amount of paint necessary to cover the surface with a single coat. The area of a shape can be measured by comparing the shape to squares of a fixed size 1 m2 or 1 cm2 etc. Every unit of length has a corresponding unit of area. We can measure areas in square meters (m2), square centimeters (cm2), square millimeters (mm2), square kilometers (km2), square feet (ft2), square yards (yd2), square miles (mi2), and so forth.The area of a shape is the “space enclosed within the perimeter or the boundary” of the given shape.
Number of problems found: 2129
- Square area
 Find the area of a square with a side length of 4/5 yards.
Find the area of a square with a side length of 4/5 yards. - Isosceles triangle
 Calculate the area of an isosceles triangle, the base measuring 16 cm and the arms 10 cm.
Calculate the area of an isosceles triangle, the base measuring 16 cm and the arms 10 cm. - Trapezium 2
 The trapezium has an area of 24 square cm. How many different trapeziums can be formed?
The trapezium has an area of 24 square cm. How many different trapeziums can be formed? - Playground
 Fencing square playground cost € 464; 1-meter cost € 19. What is the area of the playground?
Fencing square playground cost € 464; 1-meter cost € 19. What is the area of the playground?
- Area of RT 2
 Calculate the area of a right triangle whose legs have a length of 6.2 cm and 9.8 cm.
Calculate the area of a right triangle whose legs have a length of 6.2 cm and 9.8 cm. - Square
 If we increase the side of the square, increase its area of 91%. What is the percentage we increase the side of the square?
If we increase the side of the square, increase its area of 91%. What is the percentage we increase the side of the square? - Right triangle
 Right triangle ABC with side a = 19 and the area S = 95. Calculate the length of the remaining sides.
Right triangle ABC with side a = 19 and the area S = 95. Calculate the length of the remaining sides. - Right triangle
 Right triangle legs have lengths 630 mm and 411 dm. Calculate the area of this triangle.
Right triangle legs have lengths 630 mm and 411 dm. Calculate the area of this triangle. - Circumference 47983
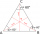 What is the area of an equilateral triangle with a circumference of 63 cm?
What is the area of an equilateral triangle with a circumference of 63 cm?
- Increase 4957
 How does the area of a circle change if we double its radius? How many times does its area increase?
How does the area of a circle change if we double its radius? How many times does its area increase? - Perimeter 2890
 The perimeter of the square is 380 dm. What will be its area?
The perimeter of the square is 380 dm. What will be its area? - The length 14
 The length of the rectangle is 6cm, and the perimeter of the rectangle is 20 cm. Find the rectangle's breadth. Find the area of the rectangle.
The length of the rectangle is 6cm, and the perimeter of the rectangle is 20 cm. Find the rectangle's breadth. Find the area of the rectangle. - A rhombus 3
 A rhombus has a side length of 6 centimeters and a height of 2 centimeters. What is the area of the rhombus in centimeters square?
A rhombus has a side length of 6 centimeters and a height of 2 centimeters. What is the area of the rhombus in centimeters square? - Annular area
 The square with side a = 1 is inscribed and circumscribed by circles. Find the annular area.
The square with side a = 1 is inscribed and circumscribed by circles. Find the annular area.
- Rectangle - area, perimeter
 The area of a rectangular field is equal to 300 square meters. Its perimeter is equal to 70 meters. Find the length and width of this rectangle.
The area of a rectangular field is equal to 300 square meters. Its perimeter is equal to 70 meters. Find the length and width of this rectangle. - CZ flag
 What percentage of the Czech flag comprises blue, white, and red textiles?
What percentage of the Czech flag comprises blue, white, and red textiles? - Square
 Calculate the square's perimeter and area with a diagonal length of 30 cm.
Calculate the square's perimeter and area with a diagonal length of 30 cm. - Perimeter from area
 What is the perimeter of the square if its area is 64 cm²?
What is the perimeter of the square if its area is 64 cm²? - Side of a square
 What is the length of the side of a square when its area is 64 cm square?
What is the length of the side of a square when its area is 64 cm square?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
