Practice problems of the volume - page 12 of 118
Number of problems found: 2345
- Calculation 81405
 Sketch the mesh of a cylinder whose base radius to height ratio is 2 : 3. Calculate the volume and surface of the cylinder if its height is 9 cm (sketch, calculation, answer).
Sketch the mesh of a cylinder whose base radius to height ratio is 2 : 3. Calculate the volume and surface of the cylinder if its height is 9 cm (sketch, calculation, answer). - Calculation 81401
 A regular four-sided pyramid has a volume of 2,160 liters and a base edge length of 12 dm. Calculate the height of the needle (sketch, calculation, answer).
A regular four-sided pyramid has a volume of 2,160 liters and a base edge length of 12 dm. Calculate the height of the needle (sketch, calculation, answer). - Quadrilateral 81385
 A regular quadrilateral pyramid with base edge length a = 15cm and height v = 21cm is given. We draw two planes parallel to the base, dividing the height of the pyramid into three equal parts. Calculate the ratio of the volumes of the 3 bodies created.
A regular quadrilateral pyramid with base edge length a = 15cm and height v = 21cm is given. We draw two planes parallel to the base, dividing the height of the pyramid into three equal parts. Calculate the ratio of the volumes of the 3 bodies created. - Minutes 81382
 The water barrel filled to 2/3 of its volume in 42 minutes. How long will it take to fill the barrel?
The water barrel filled to 2/3 of its volume in 42 minutes. How long will it take to fill the barrel? - Revolution 81339
 The rotating cone has a volume of 120 dm³. How tall is a cylinder of revolution with the same volume as a cone of revolution?
The rotating cone has a volume of 120 dm³. How tall is a cylinder of revolution with the same volume as a cone of revolution? - 100-liter 81334
 In the morning, the waiter has 200 glasses with a volume of 0.3 liters and 100 large glasses with a volume of 0.5 liters each. He starts tapping into those glasses from the 100-liter barrel. In the evening, he will have half of the small beers and a fifth
In the morning, the waiter has 200 glasses with a volume of 0.3 liters and 100 large glasses with a volume of 0.5 liters each. He starts tapping into those glasses from the 100-liter barrel. In the evening, he will have half of the small beers and a fifth - Cube-shaped 81332
 The gardener collects rainwater in a cube-shaped container with an edge length of 80 cm. How many 16-liter buckets will he fill with water from a full reservoir?
The gardener collects rainwater in a cube-shaped container with an edge length of 80 cm. How many 16-liter buckets will he fill with water from a full reservoir? - Container 81318
 The warm liquid in the container reduced its volume by 2/27 after cooling By what percent was the warm liquid's volume greater than the cooled liquid's?
The warm liquid in the container reduced its volume by 2/27 after cooling By what percent was the warm liquid's volume greater than the cooled liquid's? - Determine 81311
 The surface of the rotating cone and its base area is in the ratio 18:5. Determine the volume of the cone if its body height is 12 cm.
The surface of the rotating cone and its base area is in the ratio 18:5. Determine the volume of the cone if its body height is 12 cm. - Equilateral 81222
 A sphere is inscribed in an equilateral cone with a base diameter of 12 cm. Calculate the volume of both bodies. What percentage of the volume of the cone is filled by the inscribed sphere?
A sphere is inscribed in an equilateral cone with a base diameter of 12 cm. Calculate the volume of both bodies. What percentage of the volume of the cone is filled by the inscribed sphere? - Equilateral 81142
 The rotating body was created by rotating an equilateral triangle with a side length of a=2 cm around one of its sides. Calculate the volume of this rotating body.
The rotating body was created by rotating an equilateral triangle with a side length of a=2 cm around one of its sides. Calculate the volume of this rotating body. - Solution mixtures
 We have 1 liter of 80% solution. Every hour, pour 1 dl of the solution, add 1 dl of water (a 0% solution), and mix. What percent solution will we have after two mixings?
We have 1 liter of 80% solution. Every hour, pour 1 dl of the solution, add 1 dl of water (a 0% solution), and mix. What percent solution will we have after two mixings? - Toothpaste 81127
 How long will the roll of toothpaste be extruded from the tube if the volume of the toothpaste is 100 ml and the diameter of the opening is 8 mm?
How long will the roll of toothpaste be extruded from the tube if the volume of the toothpaste is 100 ml and the diameter of the opening is 8 mm? - Circumference 81095
 The hexagon pyramid has a circumference of 120 cm, and the length of the night edge is 25 cm. Calculate its volume.
The hexagon pyramid has a circumference of 120 cm, and the length of the night edge is 25 cm. Calculate its volume. - Cubes 81088
 How many cubes with an edge of 1 cm fit into a cube with an edge of 1 m?
How many cubes with an edge of 1 cm fit into a cube with an edge of 1 m? - Cubes 81080
 How many cubes with an edge of 1 mm fit into a cube with an edge of 1 cm?
How many cubes with an edge of 1 mm fit into a cube with an edge of 1 cm? - Calculate 81034
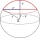 Calculate the volume of the spherical segment and the surface area of the canopy if the radius of the sphere is r=5cm and the radius of the circular base of the segment ρ=4cm.
Calculate the volume of the spherical segment and the surface area of the canopy if the radius of the sphere is r=5cm and the radius of the circular base of the segment ρ=4cm. - Quadrilateral 81033
 The foundations of a regular truncated quadrilateral pyramid are squares. The lengths of the sides differ by 6 dm. Body height is 7 dm. The body volume is 1813 dm³. Calculate the lengths of the edges of both bases.
The foundations of a regular truncated quadrilateral pyramid are squares. The lengths of the sides differ by 6 dm. Body height is 7 dm. The body volume is 1813 dm³. Calculate the lengths of the edges of both bases. - Circumscribed 81025
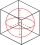 A cube with a volume of 4096 cm³ is described and inscribed by a sphere. Calculate how many times the volume of the circumscribed sphere is greater than the inscribed sphere.
A cube with a volume of 4096 cm³ is described and inscribed by a sphere. Calculate how many times the volume of the circumscribed sphere is greater than the inscribed sphere. - Cube-shaped 81023
 The cube-shaped pool is 50 m long and 16 m wide. They poured 12,000 hl of water into it. Calculate the surface area of the pool that is wetted by water.
The cube-shaped pool is 50 m long and 16 m wide. They poured 12,000 hl of water into it. Calculate the surface area of the pool that is wetted by water.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
