Volume + Pythagorean theorem - practice problems - page 2 of 15
Number of problems found: 289
- Cylinder-shaped 81512
 A truncated cone-shaped part with base radii of 4 cm and 22 cm is to be recast into a cylinder-shaped part of the same height as the original part. What base radius will the new part have?
A truncated cone-shaped part with base radii of 4 cm and 22 cm is to be recast into a cylinder-shaped part of the same height as the original part. What base radius will the new part have? - Determine 81311
 The surface of the rotating cone and its base area is in the ratio 18:5. Determine the volume of the cone if its body height is 12 cm.
The surface of the rotating cone and its base area is in the ratio 18:5. Determine the volume of the cone if its body height is 12 cm. - Equilateral 81222
 A sphere is inscribed in an equilateral cone with a base diameter of 12 cm. Calculate the volume of both bodies. What percentage of the volume of the cone is filled by the inscribed sphere?
A sphere is inscribed in an equilateral cone with a base diameter of 12 cm. Calculate the volume of both bodies. What percentage of the volume of the cone is filled by the inscribed sphere? - Equilateral 81142
 The rotating body was created by rotating an equilateral triangle with a side length of a=2 cm around one of its sides. Calculate the volume of this rotating body.
The rotating body was created by rotating an equilateral triangle with a side length of a=2 cm around one of its sides. Calculate the volume of this rotating body. - Circumference 81095
 The hexagon pyramid has a circumference of 120 cm, and the length of the night edge is 25 cm. Calculate its volume.
The hexagon pyramid has a circumference of 120 cm, and the length of the night edge is 25 cm. Calculate its volume. - Calculate 81034
 Calculate the volume of the spherical segment and the surface area of the canopy if the radius of the sphere is r=5cm and the radius of the circular base of the segment ρ=4cm.
Calculate the volume of the spherical segment and the surface area of the canopy if the radius of the sphere is r=5cm and the radius of the circular base of the segment ρ=4cm. - The perimeter
 The perimeter of the base of a regular quadrilateral pyramid is the same as its height. The pyramid has a volume of 288 dm³. Calculate its surface area round the result to the whole dm².
The perimeter of the base of a regular quadrilateral pyramid is the same as its height. The pyramid has a volume of 288 dm³. Calculate its surface area round the result to the whole dm². - One-third 77724
 The cuboid has a body diagonal u=25 cm, and side b is one-third longer than side a. What is the volume of the cuboid?
The cuboid has a body diagonal u=25 cm, and side b is one-third longer than side a. What is the volume of the cuboid? - The radius
 A right circular cone's radius and slant heights are 9 cm and 15 cm, respectively. Find, correct to one decimal place, the (i) Height (ii) Volume of the cone
A right circular cone's radius and slant heights are 9 cm and 15 cm, respectively. Find, correct to one decimal place, the (i) Height (ii) Volume of the cone - Calculate 73704
 A vertical regular 3-sided pyramid is given. The side of the base a = 5cm, and the height is 8 cm. Calculate the volume and area.
A vertical regular 3-sided pyramid is given. The side of the base a = 5cm, and the height is 8 cm. Calculate the volume and area. - Calculate 73434
 Calculate the volume and surface area of the cone with a diameter of 20 cm and a height of 15 cm.
Calculate the volume and surface area of the cone with a diameter of 20 cm and a height of 15 cm. - Equilateral 73374
 The axial section of the cone is an equilateral triangle with a side of 12 cm. Surface and volume calculation.
The axial section of the cone is an equilateral triangle with a side of 12 cm. Surface and volume calculation. - Calculate 71374
 Calculate the volume and surface of a cone whose base diameter is 6 cm and height is 0.9 dm.
Calculate the volume and surface of a cone whose base diameter is 6 cm and height is 0.9 dm. - Deviation 70744
 Calculate the volume and surface of the rotating cone if its height is 10 cm and the side has a deviation of 30 ° from the base plane.
Calculate the volume and surface of the rotating cone if its height is 10 cm and the side has a deviation of 30 ° from the base plane. - Calculate 70634
 The axial section of the cylinder is a rectangle with a diagonal of u = 20 cm. The height of the cylinder is twice the diameter of the base. Calculate the cylinder volume in liters.
The axial section of the cylinder is a rectangle with a diagonal of u = 20 cm. The height of the cylinder is twice the diameter of the base. Calculate the cylinder volume in liters. - Spherical cap
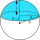 Calculate the volume of the spherical cap and the areas of the spherical canopy if r = 5 cm (radius of the sphere), ρ = 4 cm (radius of the circle of the cap).
Calculate the volume of the spherical cap and the areas of the spherical canopy if r = 5 cm (radius of the sphere), ρ = 4 cm (radius of the circle of the cap). - Quadrilateral 69834
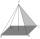 What is the volume of a regular quadrilateral pyramid? The pyramid height is 30 cm, and the wall height is 50 cm.
What is the volume of a regular quadrilateral pyramid? The pyramid height is 30 cm, and the wall height is 50 cm. - Hexagonal 66574
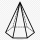 The candle is made from wax in the shape of a regular hexagonal pyramid. It has a height of 6.5 cm and a length of the base edge of 3 cm. Find the volume of wax.
The candle is made from wax in the shape of a regular hexagonal pyramid. It has a height of 6.5 cm and a length of the base edge of 3 cm. Find the volume of wax. - Right-angled 66344
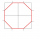 From a square with a side of 4 cm, we cut four right-angled isosceles triangles with right angles at the square's vertices and with an overlap of √2 cm. We get an octagon. Calculate its perimeter if the area of the octagon is 14 cm².
From a square with a side of 4 cm, we cut four right-angled isosceles triangles with right angles at the square's vertices and with an overlap of √2 cm. We get an octagon. Calculate its perimeter if the area of the octagon is 14 cm². - Perpendiculars 66274
 The perpendiculars of a right triangle have lengths of 30 cm and 40 cm. What is the height of the triangle?
The perpendiculars of a right triangle have lengths of 30 cm and 40 cm. What is the height of the triangle?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
