Expression of a variable from the formula - math word problems - page 26 of 132
Number of problems found: 2637
- Address on the envelope
 Jana helped mom write the addresses on the envelopes. It took her 3 minutes to write the first address and only 2 minutes to write each other. How many minutes will it take her to list the addresses (including the first one) if she works at this rate?
Jana helped mom write the addresses on the envelopes. It took her 3 minutes to write the first address and only 2 minutes to write each other. How many minutes will it take her to list the addresses (including the first one) if she works at this rate? - Original 63984
 If we reduce the length of the cube edge by 30%, this reduced cube has an area of 1176 cm². Specify the edge length and volume of the original cube.
If we reduce the length of the cube edge by 30%, this reduced cube has an area of 1176 cm². Specify the edge length and volume of the original cube. - Original 63974
 If we reduce the length of the cube edge by 30%, this cube has a reduced surface area of 1176 cm². Find the edge length and volume of the original cube.
If we reduce the length of the cube edge by 30%, this cube has a reduced surface area of 1176 cm². Find the edge length and volume of the original cube. - Assembling 63964
 Little Pavel was assembling building blocks (a cube is shaped like a cube). He wanted to build a big cube. However, he had 75 dice left, so he increased the edge by one die. Then he was missing 16 dice. How many cubes did he have in the kit?
Little Pavel was assembling building blocks (a cube is shaped like a cube). He wanted to build a big cube. However, he had 75 dice left, so he increased the edge by one die. Then he was missing 16 dice. How many cubes did he have in the kit?
- A swimmer 2
 A swimmer swam 48 kilometers in d days. What is the value of d if the swimmer swam an average of 3.2 kilometers daily?
A swimmer swam 48 kilometers in d days. What is the value of d if the swimmer swam an average of 3.2 kilometers daily? - Circumference 63814
 The KLMN diamond has a circumference of 32 cm, and the intersection of its diagonals is 3 cm away from the LM side. What is the area of the diamond?
The KLMN diamond has a circumference of 32 cm, and the intersection of its diagonals is 3 cm away from the LM side. What is the area of the diamond? - String 63794
 The chord AB is in the circle k with a radius of 13 cm. The center C of the string AB is 5 cm from the center S of the circle. How long is the AB string?
The chord AB is in the circle k with a radius of 13 cm. The center C of the string AB is 5 cm from the center S of the circle. How long is the AB string? - Triangle's 63774
 Calculate the perimeter of an isosceles triangle if the triangle's height is 15 cm and the base is 16 cm.
Calculate the perimeter of an isosceles triangle if the triangle's height is 15 cm and the base is 16 cm. - Calculate 63764
 A glass in the shape of a cylinder with a base diameter of 6 cm can hold 4dl of water. Calculate the height of the glass and its surface.
A glass in the shape of a cylinder with a base diameter of 6 cm can hold 4dl of water. Calculate the height of the glass and its surface.
- In a GP 72+144
 In a GP, the sum of the 2nd and fifth terms is 72, and the sum of the 3rd and 6th terms is 144. Find the common ratio, find the first term, and find the sum of the first six terms
In a GP, the sum of the 2nd and fifth terms is 72, and the sum of the 3rd and 6th terms is 144. Find the common ratio, find the first term, and find the sum of the first six terms - Triangle 63244
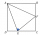 The area of the ABCD square in the picture is 36 cm². Points E and F are the centers of the square BC and CD sides. What is the area of the triangle AEF in cm²?
The area of the ABCD square in the picture is 36 cm². Points E and F are the centers of the square BC and CD sides. What is the area of the triangle AEF in cm²? - Volume 63234
 The cube with a volume of 216 l has an edge with the following:
The cube with a volume of 216 l has an edge with the following: - Observation 63194
 Determine the height of the cloud above the lake's surface if we see it from place A at an elevation angle of 20° 57'. From the same place A, we see its image in the lake at a depth angle of 24° 12'. Observation point A is 115m above the lake level.
Determine the height of the cloud above the lake's surface if we see it from place A at an elevation angle of 20° 57'. From the same place A, we see its image in the lake at a depth angle of 24° 12'. Observation point A is 115m above the lake level. - Hundredfold 63144
 The length of the radius of the rotating cylinder base is 5 m. You calculate the radius of an equally high cylinder, the volume of which is a hundredfold.
The length of the radius of the rotating cylinder base is 5 m. You calculate the radius of an equally high cylinder, the volume of which is a hundredfold.
- Sidewalk 63134
 A 2m wide sidewalk is built around the circular fountain. The radii of the circles that delimit the path on both sides are 4:3. What area in square meters does this sidewalk occupy?
A 2m wide sidewalk is built around the circular fountain. The radii of the circles that delimit the path on both sides are 4:3. What area in square meters does this sidewalk occupy? - Perimeter 63114
 The perimeter of the regular octagon is 8u + 16 cm. Calculate the side if u = 0.5 cm.
The perimeter of the regular octagon is 8u + 16 cm. Calculate the side if u = 0.5 cm. - Grandfather 63074
 My only son was born when I was 37 years old. That was exactly 32 years after the death of my grandfather, and he died at the age of 64. Dedecek was 12 years older than Grandma; they got married in 1947, just when Grandma was 18 years old. What year was m
My only son was born when I was 37 years old. That was exactly 32 years after the death of my grandfather, and he died at the age of 64. Dedecek was 12 years older than Grandma; they got married in 1947, just when Grandma was 18 years old. What year was m - Environment 62874
 Women and children have free entry to the Slavia Prague Cup football match in their home environment. The entry fee for men is CZK 85. The ratio of men, women, and children is 12:3:2. A total of CZK 431,460 was collected for tickets. Determine the total n
Women and children have free entry to the Slavia Prague Cup football match in their home environment. The entry fee for men is CZK 85. The ratio of men, women, and children is 12:3:2. A total of CZK 431,460 was collected for tickets. Determine the total n - Calculate 62864
 The block volume is 1440 cm3, its surface is 792 cm2, and the area of one of its walls is 92 cm². Calculate the lengths of its sides.
The block volume is 1440 cm3, its surface is 792 cm2, and the area of one of its walls is 92 cm². Calculate the lengths of its sides.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
