Factorial - practice problems - page 2 of 7
The factorial of the number n is the product of the first n natural numbers. For example 6! (we read 6 factorial) is 1*2*3*4*5*6 = 720.
Direction: Solve each problem carefully and show your solution in each item.
Number of problems found: 123
- Triangle from sticks
 Bob the boulder has many sticks of lengths 3.5 and 7. He wants to form triangles, each of whose edges consists of exactly one stick. How many non-congruent triangles can be formed with the sticks?
Bob the boulder has many sticks of lengths 3.5 and 7. He wants to form triangles, each of whose edges consists of exactly one stick. How many non-congruent triangles can be formed with the sticks? - Book Store
 The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w
The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w - Characters 63404
 How many characters can we create from two commas and four dots?
How many characters can we create from two commas and four dots? - Arrangements 63384
 Determine the number of arrangements of these six elements: a, a, a, b, b, c.
Determine the number of arrangements of these six elements: a, a, a, b, b, c.
- Gertrude 62304
 Six boys and six girls (among them Emil, Félix, Gertrude, and Hanka) want to dance. The number of ways they can make six (mixed) couples if Emil does not want to dance with Gertrude and Hanka wants to dance with Felix is?
Six boys and six girls (among them Emil, Félix, Gertrude, and Hanka) want to dance. The number of ways they can make six (mixed) couples if Emil does not want to dance with Gertrude and Hanka wants to dance with Felix is? - School group
 There are five girls and seven boys in the group. They sit in a row next to each other. How many options if no two girls sit next to each other?
There are five girls and seven boys in the group. They sit in a row next to each other. How many options if no two girls sit next to each other? - The flag
 The flag should consist of 3 different colored stripes - available colors: white, red, blue, green, and yellow. Specify: A) number of all flags B) number of flags with a blue stripe C) number of flags with a blue stripe in the middle D) the number of flag
The flag should consist of 3 different colored stripes - available colors: white, red, blue, green, and yellow. Specify: A) number of all flags B) number of flags with a blue stripe C) number of flags with a blue stripe in the middle D) the number of flag - Indistinguishable 48981
 How many ways can we build eight indistinguishable towers on an 8 × 8 board, so they don't endanger each other?
How many ways can we build eight indistinguishable towers on an 8 × 8 board, so they don't endanger each other? - How many 13
 How many ways can X³ y⁴ z³ be written without an exponent?
How many ways can X³ y⁴ z³ be written without an exponent?
- A department
 There are seven women and five men in a department. a) how many ways can a committee of 3 people be selected? b) how many ways can a committee of 2 men and one woman be selected? c) how many ways can a committee of at least two women be selected (3 people
There are seven women and five men in a department. a) how many ways can a committee of 3 people be selected? b) how many ways can a committee of 2 men and one woman be selected? c) how many ways can a committee of at least two women be selected (3 people - Factorial cancellation
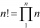 Cancel the expression with factorials: 12! x 2 x 7! / 6 x 10! 8!
Cancel the expression with factorials: 12! x 2 x 7! / 6 x 10! 8! - Megapizza
 Mega pizza will be divided among 100 people. First gets 1%, 2nd 2% of the remainder, 3rd 3% of the remainder, etc. Last 100th 100% of the remainder. Which person got the biggest portion?
Mega pizza will be divided among 100 people. First gets 1%, 2nd 2% of the remainder, 3rd 3% of the remainder, etc. Last 100th 100% of the remainder. Which person got the biggest portion? - Different 42371
 How many ways can you store seven different books side-by-side when a math book has to be on the edge of the shelf?
How many ways can you store seven different books side-by-side when a math book has to be on the edge of the shelf? - Permutations with repetitions
 How many times can the input of 1.2.2.3.3.3.4 be permutated into four digits, three digits, and two digits without repetition? Ex: 4 digits = 1223, 2213, 3122, 2313, 4321. . etc 3 digits = 122.212.213.432. . etc 2 digits = 12, 21, 31, 23 I have tried the
How many times can the input of 1.2.2.3.3.3.4 be permutated into four digits, three digits, and two digits without repetition? Ex: 4 digits = 1223, 2213, 3122, 2313, 4321. . etc 3 digits = 122.212.213.432. . etc 2 digits = 12, 21, 31, 23 I have tried the
- Cups on the shelf
 We should place two green, three red, and two yellow cups side by side on the shelf. a) How many different ways of setting up can arise? b) How many different ways of arranging can arise if cups of the same color stand side by side?
We should place two green, three red, and two yellow cups side by side on the shelf. a) How many different ways of setting up can arise? b) How many different ways of arranging can arise if cups of the same color stand side by side? - Different 38123
 How many ways can we put seven different books on the shelf?
How many ways can we put seven different books on the shelf? - Starting 38113
 How many ways can we put 19 students in a row when starting a gym?
How many ways can we put 19 students in a row when starting a gym? - Guaranteed 37611
 Determine how many different ways a Lotto ticket can be written if we guess six numbers out of 49. At what Jackpot would it already pay to bet so many tickets to be guaranteed to win the 1st prize? The price of one type is €1.
Determine how many different ways a Lotto ticket can be written if we guess six numbers out of 49. At what Jackpot would it already pay to bet so many tickets to be guaranteed to win the 1st prize? The price of one type is €1. - Arranged 37131
 Jane wants to organize 4 English and 3 Slovak books on the shelf to arrange first English and then Slovak books. How many ways can it do that?
Jane wants to organize 4 English and 3 Slovak books on the shelf to arrange first English and then Slovak books. How many ways can it do that?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
