Grade - math word problems - page 37 of 875
Number of problems found: 17498
- 7 athletes
 Seven athletes run a combined total of 4 miles. How many miles did each athlete run?
Seven athletes run a combined total of 4 miles. How many miles did each athlete run? - A bakery
 A bakery makes cylindrical mini muffins that measure 2 inches in diameter and one and one-fourth inches in height. If each mini muffin is completely wrapped in paper, then at least how much paper is needed to wrap 6 mini muffins? Approximate using pi equa
A bakery makes cylindrical mini muffins that measure 2 inches in diameter and one and one-fourth inches in height. If each mini muffin is completely wrapped in paper, then at least how much paper is needed to wrap 6 mini muffins? Approximate using pi equa - Below freeze
 What is the final temperature? 32°C is reduced by 33°C
What is the final temperature? 32°C is reduced by 33°C - Fruits
 (I) bought three apples, two oranges, four pears, and five bananas, which in total cost £3.73. (i) I bought twenty-one apples, no oranges, eight pears, and fifteen bananas, which in total cost £7.57. (i) I bought one apple, eighteen oranges, fourteen pear
(I) bought three apples, two oranges, four pears, and five bananas, which in total cost £3.73. (i) I bought twenty-one apples, no oranges, eight pears, and fifteen bananas, which in total cost £7.57. (i) I bought one apple, eighteen oranges, fourteen pear
- Calculate 397
 Calculate the surface of a spire with a base in the shape of a rectangle with dimensions of 5m and 6m. The height of the spire is 7m.
Calculate the surface of a spire with a base in the shape of a rectangle with dimensions of 5m and 6m. The height of the spire is 7m. - 3 gifts
 Chad had 30 dollars to spend on 3 gifts. He spent 9 1/4 dollars on gift A and 3 4/5 dollars on gift B. How much money did he have left for gift C?
Chad had 30 dollars to spend on 3 gifts. He spent 9 1/4 dollars on gift A and 3 4/5 dollars on gift B. How much money did he have left for gift C? - In which
 In which of the following expressions does the number 16 fill in the blank so that the equation is true? Select all that apply. A) 8(___ + 3) = 32 + 24 B) 8(2 + 9) = ___ + 72 C) 4(7 + 4) = 28 + ___ D) 8(5 + 6) = 40 + ___
In which of the following expressions does the number 16 fill in the blank so that the equation is true? Select all that apply. A) 8(___ + 3) = 32 + 24 B) 8(2 + 9) = ___ + 72 C) 4(7 + 4) = 28 + ___ D) 8(5 + 6) = 40 + ___ - What is 29
 What is the product of negative 2 and 2 over 5 and negative 3 and 5 over 6? Enter your answer as a mixed number or improper fraction in the simplest form.
What is the product of negative 2 and 2 over 5 and negative 3 and 5 over 6? Enter your answer as a mixed number or improper fraction in the simplest form. - Three 232
 Three out of eleven working mothers in a major US city have at least one child under the age of Five(5). If there are 2,250 mothers employed in that city, how many have at least one child under the age of five? (round to nearest whole number)
Three out of eleven working mothers in a major US city have at least one child under the age of Five(5). If there are 2,250 mothers employed in that city, how many have at least one child under the age of five? (round to nearest whole number)
- The rope
 Fred was learning to tie rope. He had 5 1/2 feet of rope. If each knot took up 4/5 of a foot of rope, how many knots could he make?
Fred was learning to tie rope. He had 5 1/2 feet of rope. If each knot took up 4/5 of a foot of rope, how many knots could he make? - Represent 14
 Represent 10% as a fraction reduced to the lowest term.
Represent 10% as a fraction reduced to the lowest term. - One-third of a drum
 1/3 rd of a drum is filled with water. Needed another 60 l of water to fill the whole drum, then what is the capacity of a drum?
1/3 rd of a drum is filled with water. Needed another 60 l of water to fill the whole drum, then what is the capacity of a drum? - A radio antenna
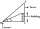 Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from
Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from - Z-score calc
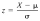 What is the Z Score for the following numbers: X is 16, and data for the population mean, and the standard deviation is 196, 193, 79, 30, 29, 81, 25, 21, 164 Level of difficulty = 2 of 2 Please format it to 2 decimal places.
What is the Z Score for the following numbers: X is 16, and data for the population mean, and the standard deviation is 196, 193, 79, 30, 29, 81, 25, 21, 164 Level of difficulty = 2 of 2 Please format it to 2 decimal places.
- Edmond 2
 Edmond bought a new cage for his pet rabbit since he's gotten so big. The area of the old cage's floor was 6 square feet. The area of the new cage's floor is n square feet larger, for a total of 8 square feet. Write expressions that tell this story and fi
Edmond bought a new cage for his pet rabbit since he's gotten so big. The area of the old cage's floor was 6 square feet. The area of the new cage's floor is n square feet larger, for a total of 8 square feet. Write expressions that tell this story and fi - Five roommates
 Five roommates will move into a house with four bedrooms: one double room and three single rooms. The five roommates propose that they draw names to determine the order in which they pick the bedrooms, assuming that the first three names drawn will choose
Five roommates will move into a house with four bedrooms: one double room and three single rooms. The five roommates propose that they draw names to determine the order in which they pick the bedrooms, assuming that the first three names drawn will choose - Ruben
 Ruben owns a restaurant. He likes to keep track of everything customers are buying. His top 3 sellers are sandwiches, salads, and pizza. He knows that 1/3 of his customers buy a sandwich, 1/2 buy a salad, and 1/4 buy a pizza. What fraction of customers bu
Ruben owns a restaurant. He likes to keep track of everything customers are buying. His top 3 sellers are sandwiches, salads, and pizza. He knows that 1/3 of his customers buy a sandwich, 1/2 buy a salad, and 1/4 buy a pizza. What fraction of customers bu - Charity
 Greg's grandmother is knitting scarves for charity. The table shows the number of yards needed for different types of scarves. Yarn Type ; Number of Yards Bulky ; 150 Light ; 250 Medium; 200 She plans to make bulky scarves and has no more than 2,250 yards
Greg's grandmother is knitting scarves for charity. The table shows the number of yards needed for different types of scarves. Yarn Type ; Number of Yards Bulky ; 150 Light ; 250 Medium; 200 She plans to make bulky scarves and has no more than 2,250 yards - Cereals
 Cole and Carl share an 18-ounce box of cereal. By the end of the week, Cole has eaten 1/6 of the box, and Carl has eaten 2/3 of the box of cereal. How many ounces are left in the box?
Cole and Carl share an 18-ounce box of cereal. By the end of the week, Cole has eaten 1/6 of the box, and Carl has eaten 2/3 of the box of cereal. How many ounces are left in the box?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
