Examples for secondary school students - page 31 of 213
Number of problems found: 4253
- Bracelet 70684
 A gold ring with a width of 1 cm is made by drilling a sphere with a radius of 1 cm through its center. A gold bracelet with a width of 1 cm is made by drilling a sphere with a radius of 4 cm through its center. Which piece of jewelry will be worth more i
A gold ring with a width of 1 cm is made by drilling a sphere with a radius of 1 cm through its center. A gold bracelet with a width of 1 cm is made by drilling a sphere with a radius of 4 cm through its center. Which piece of jewelry will be worth more i - Freezer 70664
 There are a total of 38 ducks in the freezer. Of these, 24 weigh more than 1.2, and 22 ducks weigh less than 1.5. How many ducks weigh more than 1.2 and less than 1.5 kg?
There are a total of 38 ducks in the freezer. Of these, 24 weigh more than 1.2, and 22 ducks weigh less than 1.5. How many ducks weigh more than 1.2 and less than 1.5 kg? - Calculate 70634
 The axial section of the cylinder is a rectangle with a diagonal of u = 20 cm. The height of the cylinder is twice the diameter of the base. Calculate the cylinder volume in liters.
The axial section of the cylinder is a rectangle with a diagonal of u = 20 cm. The height of the cylinder is twice the diameter of the base. Calculate the cylinder volume in liters. - Number pattern
 What are the following two numbers that occur in this pattern? 0.24, 0.48, 0.96, 1.92, ____, ____
What are the following two numbers that occur in this pattern? 0.24, 0.48, 0.96, 1.92, ____, ____ - Employees 70614
 The company has 18 employees aged 26-52. The age groups of the employees are: 3 employees aged 52 years, 2 aged 32 years, 1 ... 26 years old, 5 ... 36 years old, 4 ... 45 years old, and 3 ... 50 years old. Determine the median.
The company has 18 employees aged 26-52. The age groups of the employees are: 3 employees aged 52 years, 2 aged 32 years, 1 ... 26 years old, 5 ... 36 years old, 4 ... 45 years old, and 3 ... 50 years old. Determine the median. - Tax reports
 If 1 1/2 accountants can do 2 1/2 tax returns in 1 1/2 hours, how many tax returns can three accountants do in 3 hours?
If 1 1/2 accountants can do 2 1/2 tax returns in 1 1/2 hours, how many tax returns can three accountants do in 3 hours? - Describe 11
 Describe and correct the error in finding the difference function of (f-g) (x) of f(x) =(x²+3x-1) and g(x) =(x²+x+2) (f-g) (x) =f(x)-g(x) =(x²+3x-1) - (x²+x+2) =x²+3x-1 -x²+x+2 =x²-x²+3x+x-1+2 =4x+1
Describe and correct the error in finding the difference function of (f-g) (x) of f(x) =(x²+3x-1) and g(x) =(x²+x+2) (f-g) (x) =f(x)-g(x) =(x²+3x-1) - (x²+x+2) =x²+3x-1 -x²+x+2 =x²-x²+3x+x-1+2 =4x+1 - Function x*tanx
 Functions: f(x)=xtanx f(x)=(e^x)/((e^x)+1) Find; i)vertical and horizontal asymptotes iii)the interval of decrease and increase iii)Local maxima and local minima iv)interval of concavity and inflection. And sketch the graph.
Functions: f(x)=xtanx f(x)=(e^x)/((e^x)+1) Find; i)vertical and horizontal asymptotes iii)the interval of decrease and increase iii)Local maxima and local minima iv)interval of concavity and inflection. And sketch the graph. - Deviation 70434
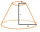 Frustum has the base radii of the figures r1 and r2: r1> r2, r2 = s, and if the side deviation from the base plane is 60°. Express the surface and volume of the cone frustum using its side s.
Frustum has the base radii of the figures r1 and r2: r1> r2, r2 = s, and if the side deviation from the base plane is 60°. Express the surface and volume of the cone frustum using its side s. - Solutions 70424
 To what extent do we need to mix 82% and 54% solutions to get a 76% solution?
To what extent do we need to mix 82% and 54% solutions to get a 76% solution? - Assemble 70414
 How many ways can we assemble five wagons when sand is in three wagons and cement in two?
How many ways can we assemble five wagons when sand is in three wagons and cement in two? - Quadrilateral 70294
 The edge lengths of a quadrilateral prism are in the ratio a: b: c = 2:4:5. The surface of the prism is 57 cm². Calculate the volume.
The edge lengths of a quadrilateral prism are in the ratio a: b: c = 2:4:5. The surface of the prism is 57 cm². Calculate the volume. - Including 70264
 A group of six, including at least three women, is selected from seven men and four women. Find how many ways we can do this.
A group of six, including at least three women, is selected from seven men and four women. Find how many ways we can do this. - Coefficient 70214
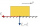 An 80 kg cart moving at constant speed along a horizontal road is subjected to a pulling force of 120 N. Specify: a) the magnitude of the frictional force b) the value of the coefficient of shear friction.
An 80 kg cart moving at constant speed along a horizontal road is subjected to a pulling force of 120 N. Specify: a) the magnitude of the frictional force b) the value of the coefficient of shear friction. - Assume
 Assume that you are to buy 5-peso worth of candy in two different stores. In your coin purse that contains two 20-peso coins, three 10-peso coins, six 5-peso coins, and seven 1-peso coins, what is the probability of getting two consecutive 5-peso coins fr
Assume that you are to buy 5-peso worth of candy in two different stores. In your coin purse that contains two 20-peso coins, three 10-peso coins, six 5-peso coins, and seven 1-peso coins, what is the probability of getting two consecutive 5-peso coins fr - Penny free fall
 A man drops a penny from the top of a 500m tall building. After t seconds, the penny has fallen a distance of s meters, where s(t)=500-5t². Determine the average velocity between 1s and 5s.
A man drops a penny from the top of a 500m tall building. After t seconds, the penny has fallen a distance of s meters, where s(t)=500-5t². Determine the average velocity between 1s and 5s. - Mr. Ofori
 Mr. Ofori starts a job with an annual salary of 6400, which increases by 240 every year. After working for eight years, Mr. Ofori was promoted to a new post with an annual salary of 9500, which increased by 360 every year. Find I. Mr. Ofori's salary in th
Mr. Ofori starts a job with an annual salary of 6400, which increases by 240 every year. After working for eight years, Mr. Ofori was promoted to a new post with an annual salary of 9500, which increased by 360 every year. Find I. Mr. Ofori's salary in th - Together 70014
 Matej and Anton are 44 years old together. Matej is twice as old as Anton was when Matej was half as old as Anton will be when Anton is 3 times older than Matej was when Matej was 3 times as old as Anton.
Matej and Anton are 44 years old together. Matej is twice as old as Anton was when Matej was half as old as Anton will be when Anton is 3 times older than Matej was when Matej was 3 times as old as Anton. - Altogether 69994
 Twelve players signed up for the squash tournament. Based on the lottery, they formed pairs, and in the first round, each pair played one match. The winners advanced to the second round, where they played each other one game at a time. How many matches we
Twelve players signed up for the squash tournament. Based on the lottery, they formed pairs, and in the first round, each pair played one match. The winners advanced to the second round, where they played each other one game at a time. How many matches we - Probability 69914
 During the exam, each student receives 30 different questions, from which he chooses 3 at random. To pass the exam, he needs to be able to answer two correctly. What is the probability that a student will pass if he mastered 70% of the questions (70% of t
During the exam, each student receives 30 different questions, from which he chooses 3 at random. To pass the exam, he needs to be able to answer two correctly. What is the probability that a student will pass if he mastered 70% of the questions (70% of t
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
