Pythagorean theorem - math word problems - page 21 of 67
The Pythagorean Theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This can be written as:c2 = a2 + b2
where c is the length of the hypotenuse, and a and b are the lengths of the other two sides.
A common proof of the Pythagorean Theorem is called the "area proof". To prove the theorem using this method, we can create a square with side length c and two smaller squares with side lengths a and b, as shown in the figure. We can then place the smaller squares next to each other to form a rectangle with area a x b. We can then see that the area of the square with side length c is equal to the sum of the areas of the smaller squares, which is equal to the area of the rectangle. This demonstrates that c2 = a2 + b2, as stated in the theorem.
Another proof is Euclidean proof which is based on the Euclidean geometry and construction of a line segment that is c and perpendicular to the line segment of a and b.
Number of problems found: 1339
- The perimeter
 The perimeter of a rhombus whose diagonal lengths are in the ratio 3:4 is 40 cm. What is its area in cm²?
The perimeter of a rhombus whose diagonal lengths are in the ratio 3:4 is 40 cm. What is its area in cm²? - Triangular land
 Jana has a rectangular garden measuring 30 meters by 72 meters that she wants to split diagonally from corner to corner using a fence. How long does her fence need to be?
Jana has a rectangular garden measuring 30 meters by 72 meters that she wants to split diagonally from corner to corner using a fence. How long does her fence need to be? - Outside point
 The square ABCD and the point E lying outside the given square are given. What is the area of the square when the distance | AE | = 2, | DE | = 5 a | BE | = 4?
The square ABCD and the point E lying outside the given square are given. What is the area of the square when the distance | AE | = 2, | DE | = 5 a | BE | = 4? - The right triangle
 In the right triangle ABC with a right angle at C, we know the side lengths AC = 9 cm and BC = 7 cm. Calculate the length of the remaining side of the triangle and the size of all angles.
In the right triangle ABC with a right angle at C, we know the side lengths AC = 9 cm and BC = 7 cm. Calculate the length of the remaining side of the triangle and the size of all angles. - Two circles
 Two circles with the same radius, r = 1, are given. The center of the second circle lies on the circumference of the first. What is the area of a square inscribed in the intersection of given circles?
Two circles with the same radius, r = 1, are given. The center of the second circle lies on the circumference of the first. What is the area of a square inscribed in the intersection of given circles? - Right angled triangle 3
 Side b = 1.5, hypotenuse angle A = 70 degrees, Angle B = 20 degrees. Find the length of its unknown sides.
Side b = 1.5, hypotenuse angle A = 70 degrees, Angle B = 20 degrees. Find the length of its unknown sides. - Diamond diagonals
 Calculate the diamond's diagonal lengths if its area is 156 cm² and the side length is 13 cm.
Calculate the diamond's diagonal lengths if its area is 156 cm² and the side length is 13 cm. - Rectangle 3-4-5
 The sides of the rectangle are in a ratio of 3:4. The length of its diagonal is 20 cm. Calculate the area of the rectangle.
The sides of the rectangle are in a ratio of 3:4. The length of its diagonal is 20 cm. Calculate the area of the rectangle. - A goat
 In the square garden of side (a), a goat is tied in the middle of one side. Calculate the length of the rope (r) so that the goat grazes exactly half the garden. If r = c * a, find the constant c.
In the square garden of side (a), a goat is tied in the middle of one side. Calculate the length of the rope (r) so that the goat grazes exactly half the garden. If r = c * a, find the constant c. - Rectangle
 The length of the rectangle is in the ratio of 5:12, and the circumference is 238 cm. Calculate the length of the diagonal and the area of the rectangle.
The length of the rectangle is in the ratio of 5:12, and the circumference is 238 cm. Calculate the length of the diagonal and the area of the rectangle. - 6 regular polygon
 A regular six-sided polygon has a side 5 cm long. Calculate its area. Compare how many more cm² (square centimeters) has a circle inscribed the 6-gon.
A regular six-sided polygon has a side 5 cm long. Calculate its area. Compare how many more cm² (square centimeters) has a circle inscribed the 6-gon. - Rectangle - parallelogram
 A rectangle is circumscribed by a circle with a radius of 5 cm. The short side of the rectangle measures 6 cm. Calculate the perimeter of a parallelogram ABCD, whose vertices are the midpoints of the sides of the rectangle.
A rectangle is circumscribed by a circle with a radius of 5 cm. The short side of the rectangle measures 6 cm. Calculate the perimeter of a parallelogram ABCD, whose vertices are the midpoints of the sides of the rectangle. - ISO trapezoid v2
 Bases of Isosceles trapezoid measured 20 cm and 4 cm, and its perimeter is 55 cm. What is the area of a trapezoid?
Bases of Isosceles trapezoid measured 20 cm and 4 cm, and its perimeter is 55 cm. What is the area of a trapezoid? - Round table
 A round table with a diameter d = 105 cm is coated by a square tablecloth with a side length 121 cm. About how many cm is the higher center of the tablecloth than its corners?
A round table with a diameter d = 105 cm is coated by a square tablecloth with a side length 121 cm. About how many cm is the higher center of the tablecloth than its corners? - R Trapezium
 Rectangular trapezium has bases 21 and 10 and area 92 cm². What is its perimeter?
Rectangular trapezium has bases 21 and 10 and area 92 cm². What is its perimeter? - Trigonometric functions
 In the right triangle is: tg α= frac(4) 2 Find the value of s and k: sin α= (s)/(√ 20) cos α= (k)/(√ 20)
In the right triangle is: tg α= frac(4) 2 Find the value of s and k: sin α= (s)/(√ 20) cos α= (k)/(√ 20) - Right-angled 79894
 Mug's handle is in the shape of a right-angled triangle with a hypotenuse of 15.8 cm and a shorter overhang of 5 cm. How tall is a mug?
Mug's handle is in the shape of a right-angled triangle with a hypotenuse of 15.8 cm and a shorter overhang of 5 cm. How tall is a mug? - Perpendiculars 66274
 The perpendiculars of a right triangle have lengths of 30 cm and 40 cm. What is the height of the triangle?
The perpendiculars of a right triangle have lengths of 30 cm and 40 cm. What is the height of the triangle? - Circle inscribed
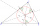 There is a triangle ABC and a circle inscribed in this triangle with a radius of 15. Point T is the point of contact of the inscribed circle with the side BC. What is the area of the triangle ABC if | BT | = 25 a | TC | = 26?
There is a triangle ABC and a circle inscribed in this triangle with a radius of 15. Point T is the point of contact of the inscribed circle with the side BC. What is the area of the triangle ABC if | BT | = 25 a | TC | = 26? - Circumference 7065
 In an isosceles triangle, the length of the base is equal to 75% of the arm's length. Determine the area of the triangle if the circumference is 22 cm.
In an isosceles triangle, the length of the base is equal to 75% of the arm's length. Determine the area of the triangle if the circumference is 22 cm.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
