Right triangle - practice for 14 year olds - page 18 of 53
Number of problems found: 1044
- Cuboid face diagonals
 The lengths of the cuboid edges are in the ratio 1:2:3. Will the lengths of its diagonals be in the same ratio? The cuboid has dimensions of 5 cm, 10 cm, and 15 cm. Calculate the size of the wall diagonals of this cuboid.
The lengths of the cuboid edges are in the ratio 1:2:3. Will the lengths of its diagonals be in the same ratio? The cuboid has dimensions of 5 cm, 10 cm, and 15 cm. Calculate the size of the wall diagonals of this cuboid. - Tangent spheres
 A sphere with a radius of 1 m is placed in the corner of the room. What is the largest sphere size that fits into the corner behind it? Additional info: Two spheres are placed in the corner of a room. The spheres are each tangent to the walls and floor an
A sphere with a radius of 1 m is placed in the corner of the room. What is the largest sphere size that fits into the corner behind it? Additional info: Two spheres are placed in the corner of a room. The spheres are each tangent to the walls and floor an - Rotary bodies
 The rotating cone and the rotary cylinder have the same volume of 180 cm³ and the same height, v = 15 cm. Which of these two bodies has a larger surface area?
The rotating cone and the rotary cylinder have the same volume of 180 cm³ and the same height, v = 15 cm. Which of these two bodies has a larger surface area? - Cylinder-shaped 4410
 A cylinder-shaped case is to be made for a ruler with the shape of a prism with a base in the shape of an equilateral triangle with a side length of 3 cm. What must be the smallest inner diameter of the housing? Determine the size to the nearest tenth of
A cylinder-shaped case is to be made for a ruler with the shape of a prism with a base in the shape of an equilateral triangle with a side length of 3 cm. What must be the smallest inner diameter of the housing? Determine the size to the nearest tenth of
- Cone side
 Calculate the volume and area of the cone whose height is 10 cm, and the axial section of the cone has an angle of 30 degrees between height and the cone side.
Calculate the volume and area of the cone whose height is 10 cm, and the axial section of the cone has an angle of 30 degrees between height and the cone side. - Equilateral cone
 We pour so much water into a container with the shape of an equilateral cone, the base of which has a radius r = 6 cm, that one-third of the volume of the cone is filled. How high will the water reach if we turn the cone upside down?
We pour so much water into a container with the shape of an equilateral cone, the base of which has a radius r = 6 cm, that one-third of the volume of the cone is filled. How high will the water reach if we turn the cone upside down? - Elevation 80869
 We can see the top of the tower standing on a plane from a certain point A at an elevation angle of 39° 25''. If we come towards its foot 50m closer to place B, we can see the top of the tower from it at an elevation angle of 56° 42''. How tall is the tow
We can see the top of the tower standing on a plane from a certain point A at an elevation angle of 39° 25''. If we come towards its foot 50m closer to place B, we can see the top of the tower from it at an elevation angle of 56° 42''. How tall is the tow - Slope of the pool
 Calculate the slope (rise:run) of the bottom of the swimming pool long 10 m. The water depth at the beginning of the pool is 0.96 m (for children), and the depth at the end is 1.86 m (for swimmers). Slope express as a percentage and as the angle in degree
Calculate the slope (rise:run) of the bottom of the swimming pool long 10 m. The water depth at the beginning of the pool is 0.96 m (for children), and the depth at the end is 1.86 m (for swimmers). Slope express as a percentage and as the angle in degree - Block-shaped 39241
 The boys wanted to store their hand-made totem 5.1 m high in the block-shaped shed, measuring 4 m, 3 m, and 2 m for the winter. Will it fit in there at all?
The boys wanted to store their hand-made totem 5.1 m high in the block-shaped shed, measuring 4 m, 3 m, and 2 m for the winter. Will it fit in there at all?
- Thales
 Calculate the length of the Thales' circle described to the right triangle with hypotenuse 44.2 cm.
Calculate the length of the Thales' circle described to the right triangle with hypotenuse 44.2 cm. - Cross road
 From the junction of two streets perpendicular to each other, two cyclists (each on another street) walked out. One ran 18 km/h and the second 24 km/h. How are they away from a) 6 minutes, b) 15 minutes?
From the junction of two streets perpendicular to each other, two cyclists (each on another street) walked out. One ran 18 km/h and the second 24 km/h. How are they away from a) 6 minutes, b) 15 minutes? - Spherical section cut
 Find the volume of a spherical section if the radius of its base is 10 cm and the magnitude of the central angle ω = 120 degrees.
Find the volume of a spherical section if the radius of its base is 10 cm and the magnitude of the central angle ω = 120 degrees. - Ratio of edges
 The cuboid dimensions are in a ratio of 3:1:2. The body diagonal has a length of 28 cm. Find the volume of a cuboid.
The cuboid dimensions are in a ratio of 3:1:2. The body diagonal has a length of 28 cm. Find the volume of a cuboid. - Ratio-cuboid
 The lengths of the edges of the cuboid are in the ratio 2: 3: 6. Its body diagonal is 14 cm long. Calculate the volume and surface area of the cuboid.
The lengths of the edges of the cuboid are in the ratio 2: 3: 6. Its body diagonal is 14 cm long. Calculate the volume and surface area of the cuboid.
- Prism
 The base of a vertical triangular prism is a right triangle with legs 4.5 cm and 6 cm long. What is the surface of the prism if its volume is 54 cubic centimeters?
The base of a vertical triangular prism is a right triangle with legs 4.5 cm and 6 cm long. What is the surface of the prism if its volume is 54 cubic centimeters? - The triangle 5
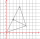 The triangle below has vertices A(-1,-2), B(2,2), and C(-1,4). What is the area of △ABCin square coordinate units?
The triangle below has vertices A(-1,-2), B(2,2), and C(-1,4). What is the area of △ABCin square coordinate units? - Forces on earth directions
 A force of 60 N [North] and 80 N [East] is exerted on an object weight of 10 kg. What is the acceleration of the object?
A force of 60 N [North] and 80 N [East] is exerted on an object weight of 10 kg. What is the acceleration of the object? - Distance
 What is the distance between the origin and the point (-11; 13)?
What is the distance between the origin and the point (-11; 13)? - Square
 Points A[9,9] and B[-4,1] are adjacent vertices of the square ABCD. Calculate the area of the square ABCD.
Points A[9,9] and B[-4,1] are adjacent vertices of the square ABCD. Calculate the area of the square ABCD.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
