Themes, topics - practice problems - page 8 of 151
This page contains thematic word problems. We have about 20 main topics, such as motion problems, mixtures, work problems etc. Please choose a specific topic that interests you from the menu. Examples within a topic usually train similar knowledge. For example, in movement tasks, terms such as distance, speed, and time often occur.Number of problems found: 3007
- Supported 82872
 An 8-meter-long swing is supported at the center. A 30 kg boy is sitting at one end. How far from the axis of rotation on the other side of the swing must the second boy of mass 40 kg sit?
An 8-meter-long swing is supported at the center. A 30 kg boy is sitting at one end. How far from the axis of rotation on the other side of the swing must the second boy of mass 40 kg sit? - Grandmother 82869
 Grandma wanted to fry steaks for lunch. So she went to buy a large piece of meat. Calculate the knife's contact area with the meat if the grandmother cut with a force of 220 N and exerted a pressure of 1.83 MPa.
Grandma wanted to fry steaks for lunch. So she went to buy a large piece of meat. Calculate the knife's contact area with the meat if the grandmother cut with a force of 220 N and exerted a pressure of 1.83 MPa. - Calculate 82808
 Calculate the radius of an iron ball with a density of 7.8g/cm³ and a mass of 7kg.
Calculate the radius of an iron ball with a density of 7.8g/cm³ and a mass of 7kg. - Simultaneously 82806
 An empty tank is filled with inflow in 30 minutes. A full tank is emptied in 75 minutes with an open drain. How long does it take for an empty tank to fill up if both the inlet and outlet are open simultaneously?
An empty tank is filled with inflow in 30 minutes. A full tank is emptied in 75 minutes with an open drain. How long does it take for an empty tank to fill up if both the inlet and outlet are open simultaneously? - Workers 82802
 Five workers do a job in 20 hours. How long will it take two workers to do the same job?
Five workers do a job in 20 hours. How long will it take two workers to do the same job? - Accumulator 82755
 The battery capacity is 50 Ah. With a current of 5A, we charge the accumulator to 100% capacity in 10 hours. To what percentage of capacity can we charge the accumulator with a current of 2A in 15 hours?
The battery capacity is 50 Ah. With a current of 5A, we charge the accumulator to 100% capacity in 10 hours. To what percentage of capacity can we charge the accumulator with a current of 2A in 15 hours? - Overtake 82752
 I am passing a tractor whose speed is 20 km/h. The length of the tractor with the siding is 10 m. My speed is 50 km/h. How long will I overtake the tractor?
I am passing a tractor whose speed is 20 km/h. The length of the tractor with the siding is 10 m. My speed is 50 km/h. How long will I overtake the tractor? - Intervention 82748
 The missile flies towards the plane at a 2000 km/h speed. The speed of the plane is 1000 km/h. The intervention is after 1.5 minutes. How far apart were the rocket and the aircraft in the beginning?
The missile flies towards the plane at a 2000 km/h speed. The speed of the plane is 1000 km/h. The intervention is after 1.5 minutes. How far apart were the rocket and the aircraft in the beginning? - Children's 82745
 The children's car has wheels with a radius of 15 cm, and its speed is 36 km/h. How many times does the toy car wheel turn in a minute at this speed?
The children's car has wheels with a radius of 15 cm, and its speed is 36 km/h. How many times does the toy car wheel turn in a minute at this speed? - Containers 82736
 Two filling machines fill 250 containers in 2 hours. How many containers will 4 machines fill in 3 hours?
Two filling machines fill 250 containers in 2 hours. How many containers will 4 machines fill in 3 hours? - Kilometers 82735
 Fifteen kilometers in front of us, a car travels at a speed of 70 km/h. We drive at an average speed of 100 km/h. How many minutes will it take us to catch up with the car?
Fifteen kilometers in front of us, a car travels at a speed of 70 km/h. We drive at an average speed of 100 km/h. How many minutes will it take us to catch up with the car? - Determine 82724
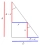 A right triangle has an area of 36 cm². A square is placed in it so that two sides of the square are parts of two sides of a triangle, and one vertex of the square is in a third of the longest side. Determine the content of this square.
A right triangle has an area of 36 cm². A square is placed in it so that two sides of the square are parts of two sides of a triangle, and one vertex of the square is in a third of the longest side. Determine the content of this square. - Kilometers 82721
 A cyclist travels at an average speed of 22 km/h. Determine how many kilometers he travels in three and a quarter hours.
A cyclist travels at an average speed of 22 km/h. Determine how many kilometers he travels in three and a quarter hours. - Resistance 82714
 A load of 23.5 ohm is connected to an ideal voltage source of 30V, and a current of 1.2A passes through the circuit. Determine the magnitude of the source's internal resistance and the short-circuit current.
A load of 23.5 ohm is connected to an ideal voltage source of 30V, and a current of 1.2A passes through the circuit. Determine the magnitude of the source's internal resistance and the short-circuit current. - Railings 82711
 Seven part-timers paint 280 m of railings in 5 hours. How many meters of railing will nine part-timers paint in 4 hours?
Seven part-timers paint 280 m of railings in 5 hours. How many meters of railing will nine part-timers paint in 4 hours? - Direction 82705
 A cyclist left Olomouc in the direction of Zábřeh in 6 h 30 min at an average speed of 24 km/h. At 7:40 a.m., a cyclist left Olomouc opposite Ostrava at an average 36 km/h rate. At what time will they be 112 km apart?
A cyclist left Olomouc in the direction of Zábřeh in 6 h 30 min at an average speed of 24 km/h. At 7:40 a.m., a cyclist left Olomouc opposite Ostrava at an average 36 km/h rate. At what time will they be 112 km apart? - Semicircle 82687
 If the shell of a cone is a semicircle, then the diameter of the cone's base is equal to its side's length. Prove it.
If the shell of a cone is a semicircle, then the diameter of the cone's base is equal to its side's length. Prove it. - Independently 82686
 Two different filling machines fill soda bottles to order. If the first machine worked alone, it would need a third less time to complete the order. How long would it take each machine to complete the job independently if the faster machine worked for 96
Two different filling machines fill soda bottles to order. If the first machine worked alone, it would need a third less time to complete the order. How long would it take each machine to complete the job independently if the faster machine worked for 96 - Different 82683
 There are candies from 1 to 10 in ten different packages. Each child took two packages. They got so many candies: Anka: 5 Zuzka: 7 Katka: 9 Monica: 15 How many candies does Lucka have?
There are candies from 1 to 10 in ten different packages. Each child took two packages. They got so many candies: Anka: 5 Zuzka: 7 Katka: 9 Monica: 15 How many candies does Lucka have? - A raft
 I want to build a raft, and I have beams with a square section with side a=20cm and length l=2m, wood density 670 kg/m³. I will connect 10 beams - what is the volume of the raft and its weight? How deep will a raft sink in water (water density 1000kg/m³)?
I want to build a raft, and I have beams with a square section with side a=20cm and length l=2m, wood density 670 kg/m³. I will connect 10 beams - what is the volume of the raft and its weight? How deep will a raft sink in water (water density 1000kg/m³)?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
