Practice problems of the triangle - page 7 of 117
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. The sum of the measures of the interior angles of a triangle is always 180 degrees. An exterior angle of a triangle is an angle that is a linear pair (and hence supplementary) to an interior angle. The best known area formula is T = a*h /2 where a is the length of the side of the triangle, and h is the height or altitude of the triangle.Number of problems found: 2321
- Equilateral triangle
 The equilateral triangle has a 23 cm long side. Calculate its area.
The equilateral triangle has a 23 cm long side. Calculate its area. - Sides of triangle
 Triangle has a circumference of 42 cm. Side a is two times shorter than side b, and side c is 2 cm longer than side a. Find the sizes of the sides of a triangle.
Triangle has a circumference of 42 cm. Side a is two times shorter than side b, and side c is 2 cm longer than side a. Find the sizes of the sides of a triangle. - Broken tree
 The tree is broken at 4 meters above the ground. The top of the tree touches the ground at a distance of 5 meters from the trunk. Calculate the original height of the tree.
The tree is broken at 4 meters above the ground. The top of the tree touches the ground at a distance of 5 meters from the trunk. Calculate the original height of the tree. - Equilateral triangle v2
 An equilateral triangle has a perimeter 36 dm. What is its area?
An equilateral triangle has a perimeter 36 dm. What is its area? - Triangle
 By calculation, determine if it is possible to construct a triangle with sides 10 21 19.
By calculation, determine if it is possible to construct a triangle with sides 10 21 19. - Sine
 In the triangle Δ ABC, if sin α =0.8 and sin β =0.6 Calculate sin γ.
In the triangle Δ ABC, if sin α =0.8 and sin β =0.6 Calculate sin γ. - Triangle
 For how many integer values of x can 5, 6, and x be the lengths of the sides of a triangle?
For how many integer values of x can 5, 6, and x be the lengths of the sides of a triangle? - Hypotenuse and height
 In a right triangle is length of the hypotenuse c = 56 cm and height hc = 4 cm. Determine the length of both triangle legs.
In a right triangle is length of the hypotenuse c = 56 cm and height hc = 4 cm. Determine the length of both triangle legs. - Triangle
 Calculate the area of the right triangle ΔABC if one leg is long 14 and its opposite angle is 59°.
Calculate the area of the right triangle ΔABC if one leg is long 14 and its opposite angle is 59°. - 3-bracket 3
 Two angles in a triangle are 90° and 60°. Has the triangle at least two equal sides?
Two angles in a triangle are 90° and 60°. Has the triangle at least two equal sides? - Equilateral 83145
 Calculate the side of an equilateral triangle if its perimeter is 132 cm.
Calculate the side of an equilateral triangle if its perimeter is 132 cm. - Calculate 68394
 The sizes of the interior angles of the triangle are in the ratio of 3:4:5. Calculate these angles.
The sizes of the interior angles of the triangle are in the ratio of 3:4:5. Calculate these angles. - Perpendiculars 46081
 Calculate the size of the hypotenuse in a triangle if its perpendiculars are 8 cm and 8.4 cm long.
Calculate the size of the hypotenuse in a triangle if its perpendiculars are 8 cm and 8.4 cm long. - One-quarter 13953
 Calculate the magnitude of the interior angles of the triangle ABC if alpha = two-fifths beta and alpha = one-quarter gamma.
Calculate the magnitude of the interior angles of the triangle ABC if alpha = two-fifths beta and alpha = one-quarter gamma. - Triangles 8306
 Find out how many triangles you create from lines 7 dm, 5 dm, 10 dm, 12 dm, and 15 dm long.
Find out how many triangles you create from lines 7 dm, 5 dm, 10 dm, 12 dm, and 15 dm long. - Calculate 3292
 The perimeter of the isosceles triangle is 32 cm. The base is 2 cm longer than the shoulder. Calculate the sides of the triangle.
The perimeter of the isosceles triangle is 32 cm. The base is 2 cm longer than the shoulder. Calculate the sides of the triangle. - Triangle 3187
 In a general triangle, the aspect ratio a: b = 2:3. What is the ratio of heights va: vb?
In a general triangle, the aspect ratio a: b = 2:3. What is the ratio of heights va: vb? - One angle 2
 One angle of a triangle measures 50°. The other two angles are in a ratio of 5:8. What are the measures of those two angles?
One angle of a triangle measures 50°. The other two angles are in a ratio of 5:8. What are the measures of those two angles? - Bisector 2
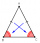 ABC is an isosceles triangle. While AB=AC, AX is the bisector of the angle ∢BAC meeting side BC at X. Prove that X is the midpoint of BC.
ABC is an isosceles triangle. While AB=AC, AX is the bisector of the angle ∢BAC meeting side BC at X. Prove that X is the midpoint of BC. - The triangle
 The triangle has sides 5 cm long, 5 cm, and 8 cm long. What is the area of the triangle?
The triangle has sides 5 cm long, 5 cm, and 8 cm long. What is the area of the triangle?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
