Volume + Pythagorean theorem - practice problems
Number of problems found: 289
- Calculate 415
 Calculate the cuboid's dimensions if the sum of its edges is 19cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm².
Calculate the cuboid's dimensions if the sum of its edges is 19cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm². - A frustum
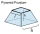 A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume.
A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume. - Quadrilateral 83324
 The volume of a regular quadrilateral pyramid is 72 cm³. Its height is equal to the length of the base edge. Calculate the length of the base and the surface of the pyramid.
The volume of a regular quadrilateral pyramid is 72 cm³. Its height is equal to the length of the base edge. Calculate the length of the base and the surface of the pyramid. - Equilateral 83322
 The glass weight has the shape of a regular four-sided pyramid with a base edge of 10 cm. The shell walls are equilateral triangles. What is the weight in grams of the paperweight if the density of the glass is 2500kg/m³?
The glass weight has the shape of a regular four-sided pyramid with a base edge of 10 cm. The shell walls are equilateral triangles. What is the weight in grams of the paperweight if the density of the glass is 2500kg/m³? - Quadrilateral 83307
 The diagonal of section DBFH of the regular quadrilateral prism ABCDEFGH inscribes a circle with a diameter of 8 cm. What is the volume of the prism?
The diagonal of section DBFH of the regular quadrilateral prism ABCDEFGH inscribes a circle with a diameter of 8 cm. What is the volume of the prism? - Quadrilateral 83272
 Calculate the surface area and volume of a regular quadrilateral pyramid whose base edge is 5 cm long and whose height is 10 cm.
Calculate the surface area and volume of a regular quadrilateral pyramid whose base edge is 5 cm long and whose height is 10 cm. - Quadrilateral 83254
 What is the volume of a regular quadrilateral pyramid if its base edge a = √18 cm and side edge b = 5 cm?
What is the volume of a regular quadrilateral pyramid if its base edge a = √18 cm and side edge b = 5 cm? - Calculate 83044
 The cube comprises 64 small cubes, each with an edge length of 15 mm. Calculate the wall length and body diagonals.
The cube comprises 64 small cubes, each with an edge length of 15 mm. Calculate the wall length and body diagonals. - Calculate 82700
 A cone of rotation with a radius of 32 cm and side length s = 65 cm is given. Calculate the surface area and volume.
A cone of rotation with a radius of 32 cm and side length s = 65 cm is given. Calculate the surface area and volume. - Calculate 82690
 A cone of rotation with a height of 18 cm and side length s = 45 cm is given. Calculate the surface area and volume.
A cone of rotation with a height of 18 cm and side length s = 45 cm is given. Calculate the surface area and volume. - Calculate 82567
 The volume of a cuboid with a square base is 64 cm3, and the body diagonal deviation from the base's plane is 45 degrees. Calculate its surface area.
The volume of a cuboid with a square base is 64 cm3, and the body diagonal deviation from the base's plane is 45 degrees. Calculate its surface area. - Calculate 82458
 Calculate the volume of a cube with a wall diagonal of u = 20 cm.
Calculate the volume of a cube with a wall diagonal of u = 20 cm. - Right-angled 82416
 What are the sides of a right-angled triangle with a perimeter of 45 centimeters and a volume of 67.5 cm²?
What are the sides of a right-angled triangle with a perimeter of 45 centimeters and a volume of 67.5 cm²? - Quadrilateral 82146
 Calculate the volume and surface area of a regular quadrilateral prism with base edge a=24 cm if the body diagonal makes an angle of 66° with the base.
Calculate the volume and surface area of a regular quadrilateral prism with base edge a=24 cm if the body diagonal makes an angle of 66° with the base. - Calculate 82073
 Calculate a cone's volume and surface area with base diameter d = 22 cm and body height v = 40 cm.
Calculate a cone's volume and surface area with base diameter d = 22 cm and body height v = 40 cm. - Quadrilateral 82066
 Calculate the volume of a regular quadrilateral pyramid with a square base of side a = 3 cm and side length b = 7 cm.
Calculate the volume of a regular quadrilateral pyramid with a square base of side a = 3 cm and side length b = 7 cm. - Inscribed 81949
 A cube is inscribed in a sphere with a radius of 27 cm. Calculate its volume and surface area.
A cube is inscribed in a sphere with a radius of 27 cm. Calculate its volume and surface area. - Cantilevers 81937
 Calculate a prism's volume and surface area with a base of a right triangle with cantilevers of length 40 and 43 cm. The height of the prism is 60 cm.
Calculate a prism's volume and surface area with a base of a right triangle with cantilevers of length 40 and 43 cm. The height of the prism is 60 cm. - Calculate 81560
 The cone's surface is 75.36 cm, and the radius is 3 cm. Calculate the volume of the cone.
The cone's surface is 75.36 cm, and the radius is 3 cm. Calculate the volume of the cone. - Spherical 81527
 Sketch a spherical layer formed from a sphere with a radius of r= 8.5cm, given: v=1.5cm, r1=7.7cm, r2=6.8cm. What is its volume?
Sketch a spherical layer formed from a sphere with a radius of r= 8.5cm, given: v=1.5cm, r1=7.7cm, r2=6.8cm. What is its volume?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
