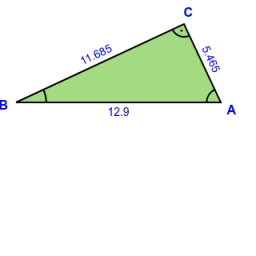
Medians in right triangle
It is given a right triangle, and angle C is 90 degrees. I know it medians t1 = 8 cm and median t2 = 12 cm. How to calculate the length of the sides?
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- quadratic equation
- equation
- expression of a variable from the formula
- planimetrics
- Pythagorean theorem
- right triangle
- triangle
- The right triangle altitude theorem
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- A right 3
 A right triangle has a perimeter of 300 cm . its hypotenuse is 130cm. What are the lengths of the other sides .
A right triangle has a perimeter of 300 cm . its hypotenuse is 130cm. What are the lengths of the other sides . - General right triangle
 In a right triangle, if a =x+34 and b = x and c= 50, then solve for x. Side c is a hypotenuse. Then discuss the case when a or b is a hypotenuse.
In a right triangle, if a =x+34 and b = x and c= 50, then solve for x. Side c is a hypotenuse. Then discuss the case when a or b is a hypotenuse. - Quadrilateral 78874
 Given is a quadrilateral ABCD inscribed in a circle, with the diagonal AC being the circle's diameter. The distance between point B and the diameter is 15 cm, and between point D and the diameter is 18 cm. Calculate the radius of the circle and the perime
Given is a quadrilateral ABCD inscribed in a circle, with the diagonal AC being the circle's diameter. The distance between point B and the diameter is 15 cm, and between point D and the diameter is 18 cm. Calculate the radius of the circle and the perime - Find all
 Find all right-angled triangles whose side lengths form an arithmetic sequence.
Find all right-angled triangles whose side lengths form an arithmetic sequence. - Side wall planes
 Find the volume and surface of a cuboid whose side c is 30 cm long and the body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls.
Find the volume and surface of a cuboid whose side c is 30 cm long and the body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls. - Similar frustums
 The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums?
The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums? - 11990 perimeter RT
 A right triangle has integer side lengths and a perimeter of 11990. In addition, we know that one of its perpendiculars has a prime number length. Find its length.
A right triangle has integer side lengths and a perimeter of 11990. In addition, we know that one of its perpendiculars has a prime number length. Find its length. - One leg
 One leg of a right triangle is 1 foot longer than the other leg. The hypotenuse is 5 feet. Find the lengths of the three sides of the triangle.
One leg of a right triangle is 1 foot longer than the other leg. The hypotenuse is 5 feet. Find the lengths of the three sides of the triangle. - A missile
 A missile is fired with a speed of 100 fps in a direction 30° above the horizontal. Determine the maximum height to which it rises. Fps foot per second.
A missile is fired with a speed of 100 fps in a direction 30° above the horizontal. Determine the maximum height to which it rises. Fps foot per second. - A Cartesian framework
 1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap
1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap - Woman's day
 We can easily make a heart for mothers for Woman's day by drawing two semicircles on the two upper sides of the square standing on their top. What is the radius of the circle circumscribed by this heart when the length of the side of the square is 1?
We can easily make a heart for mothers for Woman's day by drawing two semicircles on the two upper sides of the square standing on their top. What is the radius of the circle circumscribed by this heart when the length of the side of the square is 1? - The sides
 The sides of a right triangle form an arithmetic sequence. The hypotenuse is 24 cm long. Determine the remaining sides of the triangle.
The sides of a right triangle form an arithmetic sequence. The hypotenuse is 24 cm long. Determine the remaining sides of the triangle. - Isosceles triangle
 In an isosceles triangle ABC with base AB; A [3,4]; B [1,6] and the vertex C lies on the line 5x - 6y - 16 = 0. Calculate the coordinates of vertex C.
In an isosceles triangle ABC with base AB; A [3,4]; B [1,6] and the vertex C lies on the line 5x - 6y - 16 = 0. Calculate the coordinates of vertex C. - Perimeter and diagonal
 The perimeter of the rectangle is 82 m, and the length of its diagonal is 29 m. Find the dimensions of the rectangle.
The perimeter of the rectangle is 82 m, and the length of its diagonal is 29 m. Find the dimensions of the rectangle. - Integer sides
 A right triangle with an integer length of two sides has one leg √11 long. How much is its longest side?
A right triangle with an integer length of two sides has one leg √11 long. How much is its longest side? - Right-angled 27683
 Right-angled triangle XYZ is similar to triangle ABC, which has a right angle at the vertex X. The following applies a = 9 cm, x=4 cm, x =v-4 (v = height of triangle ABC). Calculate the missing side lengths of both triangles.
Right-angled triangle XYZ is similar to triangle ABC, which has a right angle at the vertex X. The following applies a = 9 cm, x=4 cm, x =v-4 (v = height of triangle ABC). Calculate the missing side lengths of both triangles. - Two chords
 From the point on the circle with a diameter of 8 cm, two identical chords are led, which form an angle of 60°. Calculate the length of these chords.
From the point on the circle with a diameter of 8 cm, two identical chords are led, which form an angle of 60°. Calculate the length of these chords.
