Isosceles IV
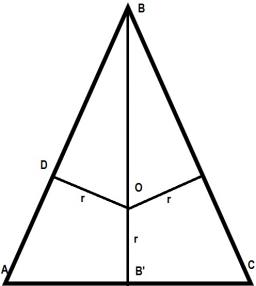
In an isosceles triangle ABC is |AC| = |BC| = 13 and |AB| = 10. Calculate the radius of the inscribed (r) and described (R) circle.
Correct answer:
Tips for related online calculators
See also our right triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Grade of the word problem:
Related math problems and questions:
- Bisector 2
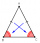 ABC is an isosceles triangle. While AB=AC, AX is the bisector of the angle ∢BAC meeting side BC at X. Prove that X is the midpoint of BC.
ABC is an isosceles triangle. While AB=AC, AX is the bisector of the angle ∢BAC meeting side BC at X. Prove that X is the midpoint of BC. - Draw triangle
 Construct an isosceles triangle ABC, if AB = 7cm, the size of the angle ABC is 47°, arms | AC | = | BC |. Measure the size of the BC side in mm.
Construct an isosceles triangle ABC, if AB = 7cm, the size of the angle ABC is 47°, arms | AC | = | BC |. Measure the size of the BC side in mm. - Triangle ABC
 In a triangle ABC with the side BC of length 2 cm. Point K is the middle point of AB. Points L and M split the AC side into three equal lines. KLM is an isosceles triangle with a right angle at point K. Determine the lengths of the sides AB, AC triangle A
In a triangle ABC with the side BC of length 2 cm. Point K is the middle point of AB. Points L and M split the AC side into three equal lines. KLM is an isosceles triangle with a right angle at point K. Determine the lengths of the sides AB, AC triangle A - Applies 14683
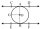 Point B is the center of the circle. The line AC touches the circles at point C and applies AB = 20 cm and AC = 16 cm. What is the radius of the circle BC?
Point B is the center of the circle. The line AC touches the circles at point C and applies AB = 20 cm and AC = 16 cm. What is the radius of the circle BC?
- Calculate 60993
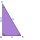 In the right triangle ABC, calculate the magnitude of the interior angles if / AB / = 13 cm; / BC / = 12 cm and / AC / = 5 cm.
In the right triangle ABC, calculate the magnitude of the interior angles if / AB / = 13 cm; / BC / = 12 cm and / AC / = 5 cm. - Isosceles - isosceles
 It is given a triangle ABC with sides /AB/ = 3 cm /BC/ = 10 cm, and the angle ABC = 120°. Draw all points X such that the BCX triangle is an isosceles and triangle ABX is an isosceles with the base AB.
It is given a triangle ABC with sides /AB/ = 3 cm /BC/ = 10 cm, and the angle ABC = 120°. Draw all points X such that the BCX triangle is an isosceles and triangle ABX is an isosceles with the base AB. - Circle inscribed
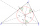 There is a triangle ABC and a circle inscribed in this triangle with a radius of 15. Point T is the point of contact of the inscribed circle with the side BC. What is the area of the triangle ABC if | BT | = 25 a | TC | = 26?
There is a triangle ABC and a circle inscribed in this triangle with a radius of 15. Point T is the point of contact of the inscribed circle with the side BC. What is the area of the triangle ABC if | BT | = 25 a | TC | = 26? - Similarity of triangles
 If triangle ABC ~ to triangle XYZ, AC = 24, AB = 15, BC = 17, and XY = 9, what is the perimeter of triangle XYZ? Round all sides to 1 decimal place.
If triangle ABC ~ to triangle XYZ, AC = 24, AB = 15, BC = 17, and XY = 9, what is the perimeter of triangle XYZ? Round all sides to 1 decimal place. - Hypotenuse 65744
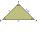 Construct a right triangle ABC with the hypotenuse AB: a) | AB | = 72 mm, | BC | = 51 mm b) | AB | = 58 mm, | AC | = 42 mm
Construct a right triangle ABC with the hypotenuse AB: a) | AB | = 72 mm, | BC | = 51 mm b) | AB | = 58 mm, | AC | = 42 mm
- Coordinates 32183
 The triangle ABC is given in the plane. A (-3,5), B (2,3), C (-1, -2) write the coordinates of the vectors u, v, w if u = AB, v = AC, and w = BC. Enter the coordinates of the centers of the lines SAB (..), SAC (...), SBC (. ..)
The triangle ABC is given in the plane. A (-3,5), B (2,3), C (-1, -2) write the coordinates of the vectors u, v, w if u = AB, v = AC, and w = BC. Enter the coordinates of the centers of the lines SAB (..), SAC (...), SBC (. ..) - Calculate 3209
 Calculate the lengths of the sides of the triangle ABC, in which angles α = 113°, β = 48°, and the radius of the circle of the triangle described is r = 10 cm.
Calculate the lengths of the sides of the triangle ABC, in which angles α = 113°, β = 48°, and the radius of the circle of the triangle described is r = 10 cm. - Sin cos tan
 In triangle ABC, right-angled at B. Sides/AB/=7cm, /BC/=5cm, /AC/=8.6cm. Find two decimal places. A. Sine C B. Cosine C C. Tangent C.
In triangle ABC, right-angled at B. Sides/AB/=7cm, /BC/=5cm, /AC/=8.6cm. Find two decimal places. A. Sine C B. Cosine C C. Tangent C. - Equilateral 4301
 Triangle ABC is equilateral with a side length of 8 cm. Points D, E, and F are the sides AB, BC, and AC midpoints. Calculate the area of triangle DEF. In what ratio is the area of triangle ABC to the area of triangle DEF?
Triangle ABC is equilateral with a side length of 8 cm. Points D, E, and F are the sides AB, BC, and AC midpoints. Calculate the area of triangle DEF. In what ratio is the area of triangle ABC to the area of triangle DEF? - Quadrilateral 3262
 Construct a quadrilateral ABCD with dimensions AB, BC, AC, BD, and angle d = CDA.
Construct a quadrilateral ABCD with dimensions AB, BC, AC, BD, and angle d = CDA.
- Calculate 16223
 The following elements are known in the right triangle ABC: a = 10 cm, height to side c h = 9.23 cm. Calculate o, R (radius of the inscribed circle), r (radius of the inscribed circle).
The following elements are known in the right triangle ABC: a = 10 cm, height to side c h = 9.23 cm. Calculate o, R (radius of the inscribed circle), r (radius of the inscribed circle). - Nonagon
 Calculate the area and perimeter of a regular nonagon if its radius of the inscribed circle is r = 10cm
Calculate the area and perimeter of a regular nonagon if its radius of the inscribed circle is r = 10cm - Hypotenuses 83154
 In a right-angled triangle ABC with a right angle at the vertex C, the magnitudes of the hypotenuses are given ta=5, tb=2√10. Calculate the side sizes of triangle ABC and the circle's radius described by this triangle.
In a right-angled triangle ABC with a right angle at the vertex C, the magnitudes of the hypotenuses are given ta=5, tb=2√10. Calculate the side sizes of triangle ABC and the circle's radius described by this triangle.
