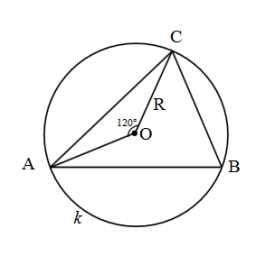
Circular railway
The railway connects in a circular arc the points A, B, and C, whose distances are | AB | = 30 km, AC = 95 km, BC | = 70 km. How long will the track be from A to C?
Correct answer:
Tips for related online calculators
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- planimetrics
- circle
- area of a shape
- perimeter
- triangle
- The Law of Cosines
- Heron's formula
- basic functions
- reason
- goniometry and trigonometry
- arccosine
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- The perimeter
 The perimeter of a rhombus whose diagonal lengths are in the ratio 3:4 is 40 cm. What is its area in cm²?
The perimeter of a rhombus whose diagonal lengths are in the ratio 3:4 is 40 cm. What is its area in cm²? - The triangle 5
 The triangle below has vertices A(-1,-2), B(2,2), and C(-1,4). What is the area of △ABCin square coordinate units?
The triangle below has vertices A(-1,-2), B(2,2), and C(-1,4). What is the area of △ABCin square coordinate units? - Trapezoid and diagonals
 Find the area of a trapezoid with bases a = 24 cm, c = 16 cm, and diagonals u = 22 cm, v = 26 cm.
Find the area of a trapezoid with bases a = 24 cm, c = 16 cm, and diagonals u = 22 cm, v = 26 cm. - Circle inscribed
 There is a triangle ABC and a circle inscribed in this triangle with a radius of 15. Point T is the point of contact of the inscribed circle with the side BC. What is the area of the triangle ABC if | BT | = 25 a | TC | = 26?
There is a triangle ABC and a circle inscribed in this triangle with a radius of 15. Point T is the point of contact of the inscribed circle with the side BC. What is the area of the triangle ABC if | BT | = 25 a | TC | = 26?
- Parallelogram ABCD
 We have the parallelogram ABCD, where AB is 6.2 cm BC is 5.4 cm AC is 4.8 cm calculate the height on the AB side and the angle DAB
We have the parallelogram ABCD, where AB is 6.2 cm BC is 5.4 cm AC is 4.8 cm calculate the height on the AB side and the angle DAB - Calculate triangle
 In the triangle, ABC, calculate the sizes of all heights, angles, perimeters, and area if given a=40cm, b=57cm, and c=59cm.
In the triangle, ABC, calculate the sizes of all heights, angles, perimeters, and area if given a=40cm, b=57cm, and c=59cm. - Irregular hexagon
 There is an irregular hexagon whose sides are the same length. The opposite sides are parallel; their distance is 237, 195, and193. What is its area?
There is an irregular hexagon whose sides are the same length. The opposite sides are parallel; their distance is 237, 195, and193. What is its area? - A Cartesian framework
 1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap
1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap - A rhombus 2
 A rhombus has sides of 170 meters and a diagonal of 300 meters. What is the area of the rhombus?
A rhombus has sides of 170 meters and a diagonal of 300 meters. What is the area of the rhombus?
- Four sides of trapezoid
 Calculate the area of the ABCD trapezoid with sides a = 65 cm, b = 29 cm, c = 40 cm, d = 36 cm
Calculate the area of the ABCD trapezoid with sides a = 65 cm, b = 29 cm, c = 40 cm, d = 36 cm - Gardens
 The area of the square garden is 3/4 of the area of the triangular garden with sides of 80 m, 50 m, and 50 m. How many meters of fence do we need to fence a square garden?
The area of the square garden is 3/4 of the area of the triangular garden with sides of 80 m, 50 m, and 50 m. How many meters of fence do we need to fence a square garden? - Vertex points
 Suppose the following points of a triangle: P(-12,6), Q(4,0), R(-8,-6). Graph the triangle. Find the triangle area.
Suppose the following points of a triangle: P(-12,6), Q(4,0), R(-8,-6). Graph the triangle. Find the triangle area. - Quadrilateral oblique prism
 What is the volume of a quadrilateral oblique prism with base edges of length a = 1m, b = 1.1m, c = 1.2m, d = 0.7m if a side edge of length h = 3.9m has a deviation from the base of 20° 35' and the edges a, b form an angle of 50.5°?
What is the volume of a quadrilateral oblique prism with base edges of length a = 1m, b = 1.1m, c = 1.2m, d = 0.7m if a side edge of length h = 3.9m has a deviation from the base of 20° 35' and the edges a, b form an angle of 50.5°? - Annulus from triangle
 Calculate the area of the area bounded by a circle circumscribed and a circle inscribed by a triangle with sides a = 25mm, b = 29mm, c = 36mm
Calculate the area of the area bounded by a circle circumscribed and a circle inscribed by a triangle with sides a = 25mm, b = 29mm, c = 36mm
- Compute 4
 Compute the exact value of the triangle area with sides 14 mi, 12 mi, and 12 mi long.
Compute the exact value of the triangle area with sides 14 mi, 12 mi, and 12 mi long. - Triangle's 9731
 Solve the triangle ABC if the side a = 52 cm, the height on the other side is vb = 21 cm, and the triangle's area is S = 330 cm².
Solve the triangle ABC if the side a = 52 cm, the height on the other side is vb = 21 cm, and the triangle's area is S = 330 cm². - Parallelogram
 The sides of the parallelogram are 8 cm and 6 cm long, and the diagonals' angle is 60°. What is its area?
The sides of the parallelogram are 8 cm and 6 cm long, and the diagonals' angle is 60°. What is its area?
