Tangents
To circle with a radius of 41 cm from the point R guided two tangents. The distance of both points of contact is 16 cm. Calculate the distance from point R and circle center.
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Quadrilateral 78874
 Given is a quadrilateral ABCD inscribed in a circle, with the diagonal AC being the circle's diameter. The distance between point B and the diameter is 15 cm, and between point D and the diameter is 18 cm. Calculate the radius of the circle and the perime
Given is a quadrilateral ABCD inscribed in a circle, with the diagonal AC being the circle's diameter. The distance between point B and the diameter is 15 cm, and between point D and the diameter is 18 cm. Calculate the radius of the circle and the perime - Touch circle
 Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l
Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l - RT sides
 Find the sides of a rectangular triangle if legs a + b = 17cm and the radius of the written circle ρ = 2cm.
Find the sides of a rectangular triangle if legs a + b = 17cm and the radius of the written circle ρ = 2cm. - Same area
 There is a given triangle. Construct a square of the same area.
There is a given triangle. Construct a square of the same area. - Hypotenuse - RT
 A triangle has a hypotenuse of 55 and an altitude to the hypotenuse of 33. What is the area of the triangle?
A triangle has a hypotenuse of 55 and an altitude to the hypotenuse of 33. What is the area of the triangle? - Circles
 In the circle with a radius, 7.5 cm is constructed of two parallel chords whose lengths are 9 cm and 12 cm. Calculate the distance of these chords (if there are two possible solutions, write both).
In the circle with a radius, 7.5 cm is constructed of two parallel chords whose lengths are 9 cm and 12 cm. Calculate the distance of these chords (if there are two possible solutions, write both). - Goat and circles
 What is the radius of a circle centered on the other circle, and is the intersection of the two circles equal to half the area of the first circle? This task is the mathematical expression of the role of agriculture. The farmer has circular land on which
What is the radius of a circle centered on the other circle, and is the intersection of the two circles equal to half the area of the first circle? This task is the mathematical expression of the role of agriculture. The farmer has circular land on which - Isosceles IV
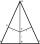 In an isosceles triangle ABC is |AC| = |BC| = 13 and |AB| = 10. Calculate the radius of the inscribed (r) and described (R) circle.
In an isosceles triangle ABC is |AC| = |BC| = 13 and |AB| = 10. Calculate the radius of the inscribed (r) and described (R) circle. - The bridge
 Across the circle, the lake passes through its center bridge over the lake. At three different locations on the lakeshore are three fishermen, A, B, and C. Which of the fishermen see the bridge from the largest angle?
Across the circle, the lake passes through its center bridge over the lake. At three different locations on the lakeshore are three fishermen, A, B, and C. Which of the fishermen see the bridge from the largest angle? - Rhombus and inscribed circle
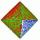 It is given a rhombus with side a = 6 cm and the radius of the inscribed circle r = 2 cm. Calculate the length of its two diagonals.
It is given a rhombus with side a = 6 cm and the radius of the inscribed circle r = 2 cm. Calculate the length of its two diagonals. - Rhombus
 It is given a rhombus of side length a = 20 cm. Touchpoints of inscribed circle divided his sides into sections a1 = 13 cm and a2 = 7 cm. Calculate the radius r of the circle and the length of the diagonals of the rhombus.
It is given a rhombus of side length a = 20 cm. Touchpoints of inscribed circle divided his sides into sections a1 = 13 cm and a2 = 7 cm. Calculate the radius r of the circle and the length of the diagonals of the rhombus. - Circle in rhombus
 In the rhombus is an inscribed circle. Contact points of touch divide the sides into parts of length 14 mm and 9 mm. Calculate the circle area.
In the rhombus is an inscribed circle. Contact points of touch divide the sides into parts of length 14 mm and 9 mm. Calculate the circle area. - Concentric circles 4
 One circle has a radius of 98 cm, and a second concentric circle has a 1m 26 cm radius. How much longer is the circumference of the second circle than that of the first?
One circle has a radius of 98 cm, and a second concentric circle has a 1m 26 cm radius. How much longer is the circumference of the second circle than that of the first? - ET inscribed circle
 An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region.
An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region. - Geometric Solid
 A concrete pipe is 1.0 m long. Its inside and outside diameters are 60 cm and 75 cm, respectively. What is the volume of the concrete (cubic meters) needed to make 25 pcs of pipe?
A concrete pipe is 1.0 m long. Its inside and outside diameters are 60 cm and 75 cm, respectively. What is the volume of the concrete (cubic meters) needed to make 25 pcs of pipe? - Vertex of the rectangle
 Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0
Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0 - Circle - analytics geometry
 Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0.
Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0.
