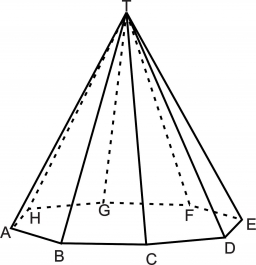
Octagonal pyramid
Find the volume of a regular octagonal pyramid with height v = 100 and the angle of the side edge with the base plane is α = 60°.
Correct answer:
Tips for related online calculators
See also our right triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- solid geometry
- pyramid
- planimetrics
- right triangle
- polygon
- area of a shape
- triangle
- goniometry and trigonometry
- tangent
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Ratio iso triangle
 The ratio of the sides of an isosceles triangle is 7:6:7. Find the base angle to the nearest answer correct to 3 significant figures.
The ratio of the sides of an isosceles triangle is 7:6:7. Find the base angle to the nearest answer correct to 3 significant figures. - Trapezoid MO
 The rectangular trapezoid ABCD with the right angle at point B, |AC| = 12, |CD| = 8, diagonals are perpendicular to each other. Calculate the perimeter and area of the trapezoid.
The rectangular trapezoid ABCD with the right angle at point B, |AC| = 12, |CD| = 8, diagonals are perpendicular to each other. Calculate the perimeter and area of the trapezoid. - Three pillars
 On a straight road, three pillars are 6 m high at the same distance of 10 m. At what angle of view does Vlado see each pillar if it is 30 m from the first and his eyes are 1.8 m high?
On a straight road, three pillars are 6 m high at the same distance of 10 m. At what angle of view does Vlado see each pillar if it is 30 m from the first and his eyes are 1.8 m high? - Subtract polar forms
 Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form
Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form - Let z 2
 Let z = 2 - sqrt(3i). Find z6 and express your answer in rectangular form. if z = 2 - 2sqrt(3 i) then r = |z| = sqrt(2 ^ 2 + (- 2sqrt(3)) ^ 2) = sqrt(16) = 4 and theta = tan -2√3/2=-π/3
Let z = 2 - sqrt(3i). Find z6 and express your answer in rectangular form. if z = 2 - 2sqrt(3 i) then r = |z| = sqrt(2 ^ 2 + (- 2sqrt(3)) ^ 2) = sqrt(16) = 4 and theta = tan -2√3/2=-π/3 - In the desert
 A man wondering in the desert walks 5.7 miles in the direction S 26° W. He then turns 90° and walks 9 miles in the direction N 49° W. At that time, how far is he from his starting point, and what is his bearing from his starting point?
A man wondering in the desert walks 5.7 miles in the direction S 26° W. He then turns 90° and walks 9 miles in the direction N 49° W. At that time, how far is he from his starting point, and what is his bearing from his starting point? - Crosswind
 A plane is traveling 45 degrees N of E at 320 km/h when it comes across a current from S of E at 115 degrees of 20 km/h. What are the airplane's new course and speed?
A plane is traveling 45 degrees N of E at 320 km/h when it comes across a current from S of E at 115 degrees of 20 km/h. What are the airplane's new course and speed? - Sin cos tan
 If cos y = 0.8, 0° ≤ y ≤ 90°, find the value of (4 tan y) / (cos y-sin y)
If cos y = 0.8, 0° ≤ y ≤ 90°, find the value of (4 tan y) / (cos y-sin y) - Subtracting complex in polar
 Given w =√2(cosine (pi/4) + i sine (pi/4) ) and z = 2 (cosine (pi/2) + i sine (pi/2) ). What is w - z expressed in polar form?
Given w =√2(cosine (pi/4) + i sine (pi/4) ) and z = 2 (cosine (pi/2) + i sine (pi/2) ). What is w - z expressed in polar form? - The body
 The body slides down an inclined plane, forming an angle α = π / 4 = 45° under the action of a horizontal plane under the effect of friction forces with acceleration a = 2.4 m/s². At what angle β must the plane be inclined so that the body slides on it af
The body slides down an inclined plane, forming an angle α = π / 4 = 45° under the action of a horizontal plane under the effect of friction forces with acceleration a = 2.4 m/s². At what angle β must the plane be inclined so that the body slides on it af - Space diagonal angles
 Calculate the angle between the body diagonal and the side edge c of the block with dimensions: a = 28cm, b = 45cm, and c = 73cm. Then, find the angle between the body diagonal and the plane of the base ABCD.
Calculate the angle between the body diagonal and the side edge c of the block with dimensions: a = 28cm, b = 45cm, and c = 73cm. Then, find the angle between the body diagonal and the plane of the base ABCD. - Triangle in a square
 In a square ABCD with side a = 6 cm, point E is the center of side AB, and point F is the center of side BC. Calculate the size of all angles of the triangle DEF and the lengths of its sides.
In a square ABCD with side a = 6 cm, point E is the center of side AB, and point F is the center of side BC. Calculate the size of all angles of the triangle DEF and the lengths of its sides. - The rescue helicopter
 The rescue helicopter is above the landing site at a height of 180m. The rescue operation site can be seen from here at a depth angle of 52°40'. How far will the helicopter land from the rescue site?
The rescue helicopter is above the landing site at a height of 180m. The rescue operation site can be seen from here at a depth angle of 52°40'. How far will the helicopter land from the rescue site? - Tetrahedral pyramid
 Determine the surface of a regular tetrahedral pyramid when its volume is V = 120 and the angle of the sidewall with the base plane is α = 42° 30'.
Determine the surface of a regular tetrahedral pyramid when its volume is V = 120 and the angle of the sidewall with the base plane is α = 42° 30'. - The aspect ratio
 The aspect ratio of the rectangular triangle is 13:12:5. Calculate the internal angles of the triangle.
The aspect ratio of the rectangular triangle is 13:12:5. Calculate the internal angles of the triangle. - Coordinates of square vertices
 I have coordinates of square vertices A / -3; 1/and B/1; 4 /. Find coordinates of vertices C and D, C and D. Thanks, Peter.
I have coordinates of square vertices A / -3; 1/and B/1; 4 /. Find coordinates of vertices C and D, C and D. Thanks, Peter. - Roof angle
 The house's roof has the shape of an isosceles triangle with arms 4 m long and the size of the base 6 m. How big an angle alpha does its roof make?
The house's roof has the shape of an isosceles triangle with arms 4 m long and the size of the base 6 m. How big an angle alpha does its roof make?
