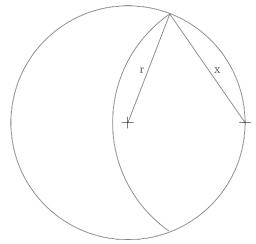
Goat and circles
What is the radius of a circle centered on the other circle, and is the intersection of the two circles equal to half the area of the first circle?
This task is the mathematical expression of the role of agriculture. The farmer has circular land on which graze goats. Because the farmer wants to spend the grass throughout the two days, tie it to a stake on the edge of the circle and length of rope for the first half of the grass. The second day gives they a whole circle where they can feed off the remaining one-half of the grass.
This task is the mathematical expression of the role of agriculture. The farmer has circular land on which graze goats. Because the farmer wants to spend the grass throughout the two days, tie it to a stake on the edge of the circle and length of rope for the first half of the grass. The second day gives they a whole circle where they can feed off the remaining one-half of the grass.
Correct answer:
Tips for related online calculators
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
You need to know the following knowledge to solve this word math problem:
- algebra
- equation
- planimetrics
- circle
- area of a shape
- The right triangle altitude theorem
- circular sector
- goniometry and trigonometry
- sine
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Touch circle
 Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l
Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l - Square equal rhombus
 Construct a square that has the same area as a rhombus ABCD if |AB| = 5cm, |AD| = 4cm and angle |DAB| = 30°.
Construct a square that has the same area as a rhombus ABCD if |AB| = 5cm, |AD| = 4cm and angle |DAB| = 30°. - Free space in the garden
 The grandfather's free space in the garden was in the shape of a rectangular triangle of 5 meters and 12 meters in length. He decided to divide it into two parts and the height of the hypotenuse. The smaller part creates a rock garden, for the larger sows
The grandfather's free space in the garden was in the shape of a rectangular triangle of 5 meters and 12 meters in length. He decided to divide it into two parts and the height of the hypotenuse. The smaller part creates a rock garden, for the larger sows - Squares above sides
 Two squares are constructed on two sides of the ABC triangle. The square area above the BC side is 25 cm². The height vc to the side AB is 3 cm long. The heel P of height vc divides the AB side in a 2: 1 ratio. The AC side is longer than the BC side. Calc
Two squares are constructed on two sides of the ABC triangle. The square area above the BC side is 25 cm². The height vc to the side AB is 3 cm long. The heel P of height vc divides the AB side in a 2: 1 ratio. The AC side is longer than the BC side. Calc
- Isosceles triangle 9
 There is an isosceles triangle ABC where AB= AC. The perimeter is 64cm, and the altitude is 24cm. Find the area of the isosceles triangle.
There is an isosceles triangle ABC where AB= AC. The perimeter is 64cm, and the altitude is 24cm. Find the area of the isosceles triangle. - Right isosceles triangle
 The right isosceles triangle has an altitude x drawn from the right angle to the hypotenuse dividing it into two equal segments. The length of one segment is 5 cm. What is the area of the triangle?
The right isosceles triangle has an altitude x drawn from the right angle to the hypotenuse dividing it into two equal segments. The length of one segment is 5 cm. What is the area of the triangle? - Hypotenuse - RT
 A triangle has a hypotenuse of 55 and an altitude to the hypotenuse of 33. What is the area of the triangle?
A triangle has a hypotenuse of 55 and an altitude to the hypotenuse of 33. What is the area of the triangle? - Sides of the triangle
 Calculate triangle sides where its area is S = 84 cm² and a = x, b = x + 1, xc = x + 2
Calculate triangle sides where its area is S = 84 cm² and a = x, b = x + 1, xc = x + 2 - Euklid4
 The legs of a right triangle have dimensions 244 m and 246 m. Calculate the length of the hypotenuse and the height of this right triangle.
The legs of a right triangle have dimensions 244 m and 246 m. Calculate the length of the hypotenuse and the height of this right triangle.
- Without Euclid laws
 Right triangle ABC with a right angle at the C has a=14 and hypotenuse c=26. Calculate the height h of this triangle without the use of Euclidean laws.
Right triangle ABC with a right angle at the C has a=14 and hypotenuse c=26. Calculate the height h of this triangle without the use of Euclidean laws. - Right Δ
 A right triangle has the length of one leg 72 cm and the hypotenuse 90 cm size. Calculate the height of the triangle.
A right triangle has the length of one leg 72 cm and the hypotenuse 90 cm size. Calculate the height of the triangle. - Area of RT
 Calculate the right triangle area that hypotenuse has length 14, and one hypotenuse segment has length 5.
Calculate the right triangle area that hypotenuse has length 14, and one hypotenuse segment has length 5. - Circle in rhombus
 In the rhombus is an inscribed circle. Contact points of touch divide the sides into parts of length 14 mm and 9 mm. Calculate the circle area.
In the rhombus is an inscribed circle. Contact points of touch divide the sides into parts of length 14 mm and 9 mm. Calculate the circle area. - A park on map
 A park has an area of ⅙ mi². On a map, the park has an area of 1 ¼ cm². On the map, how many square centimeters represent 1 mi²?
A park has an area of ⅙ mi². On a map, the park has an area of 1 ¼ cm². On the map, how many square centimeters represent 1 mi²?
- The rectangle 7
 The rectangle shown has a length (l) of 8 and a width (w) of 6.2. A second rectangle has a length of l + 2.5 and a width of w - 1.4. Find the area of the SECOND rectangle.
The rectangle shown has a length (l) of 8 and a width (w) of 6.2. A second rectangle has a length of l + 2.5 and a width of w - 1.4. Find the area of the SECOND rectangle. - A room
 A room is 8 2/3 m by 5 1/4 m. What is the area of the room?
A room is 8 2/3 m by 5 1/4 m. What is the area of the room? - Height of the box
 The box needs to have a volume of 108 ¾ cubic inches. If the width of the box is going to be 7 ¼ inches, and depth of the box is going to be 1 ¼ inches, what must the height of the box be?
The box needs to have a volume of 108 ¾ cubic inches. If the width of the box is going to be 7 ¼ inches, and depth of the box is going to be 1 ¼ inches, what must the height of the box be?
