TV competition
In the competition, ten contestants answer five questions, one question per round. Anyone who answers correctly will receive as many points as the number of competitors who answered incorrectly in that round.
After the contest, one of the contestants said: We got 116 points in total, of which I was 30.
a. In how many rounds did all competitors respond correctly?
b. In how many rounds did at least five competitors respond correctly?
c. In how many rounds did three competitors respond correctly?
After the contest, one of the contestants said: We got 116 points in total, of which I was 30.
a. In how many rounds did all competitors respond correctly?
b. In how many rounds did at least five competitors respond correctly?
c. In how many rounds did three competitors respond correctly?
Correct answer:

Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Do you solve Diofant problems and looking for a calculator of Diofant integer equations?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Do you solve Diofant problems and looking for a calculator of Diofant integer equations?
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Ten boys
 Ten boys chose to go to the supermarket. Six boys bought gum, and nine boys bought a lollipop. How many boys bought gum and a lollipop?
Ten boys chose to go to the supermarket. Six boys bought gum, and nine boys bought a lollipop. How many boys bought gum and a lollipop? - Hens and pigs
 Hens and pigs have 46 feet in total. At least how much can heads have?
Hens and pigs have 46 feet in total. At least how much can heads have? - Classmates
 Roman is ranked 12th highest and eleventh lowest pupil. How many classmates does Roman have?
Roman is ranked 12th highest and eleventh lowest pupil. How many classmates does Roman have? - Endless lego set
 The endless lego set contains only 6, 9, and 20-kilogram blocks that can no longer be polished or broken. The workers took them to the gym and immediately started building different buildings. And, of course, they wrote down how much the building weighed.
The endless lego set contains only 6, 9, and 20-kilogram blocks that can no longer be polished or broken. The workers took them to the gym and immediately started building different buildings. And, of course, they wrote down how much the building weighed. - Skoda cars
 There were 16 passenger cars in the parking. It was the ten blue and 10 Skoda cars. How many are blue Skoda cars in the parking?
There were 16 passenger cars in the parking. It was the ten blue and 10 Skoda cars. How many are blue Skoda cars in the parking? - Z9–I–1
 In all nine fields of given shape to be filled with natural numbers so that: • each of the numbers 2, 4, 6, and 8 is used at least once, • four of the inner square boxes containing the products of the numbers of adjacent cells of the outer square, • in th
In all nine fields of given shape to be filled with natural numbers so that: • each of the numbers 2, 4, 6, and 8 is used at least once, • four of the inner square boxes containing the products of the numbers of adjacent cells of the outer square, • in th - Trousers
 In the class were 12 students. Nine students were wearing trousers and turtlenecks eight. How many students wore trousers with a turtleneck?
In the class were 12 students. Nine students were wearing trousers and turtlenecks eight. How many students wore trousers with a turtleneck? - Florist's
 The flower shop has 72 white and 90 red roses. How many identical bouquets can they most tie together so that all the roses are used?
The flower shop has 72 white and 90 red roses. How many identical bouquets can they most tie together so that all the roses are used? - Cookies
 In the box were a total of 200 cookies. These products have sugar and chocolate toppings. The chocolate topping is used on 157 cookies. Sugar topping is used on 100 cakes. How many of these cookies have two frostings?
In the box were a total of 200 cookies. These products have sugar and chocolate toppings. The chocolate topping is used on 157 cookies. Sugar topping is used on 100 cakes. How many of these cookies have two frostings? - Camp
 In a class are 36 children. During the holidays, 20 children were in the camps and 18 children on holiday with their parents. Find the minimum and the maximum number of children that may have been in the camp and on holiday with their parents at the same
In a class are 36 children. During the holidays, 20 children were in the camps and 18 children on holiday with their parents. Find the minimum and the maximum number of children that may have been in the camp and on holiday with their parents at the same - Three numbers
 Create from digits 1-9 three-digit numbers with their sum the smallest. What value is the sum of these numbers? (Use each digit only once)
Create from digits 1-9 three-digit numbers with their sum the smallest. What value is the sum of these numbers? (Use each digit only once) - Circumferences 83111
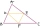 Péta composed several planar shapes from mutually congruent triangles. The circumferences of the first three are 8 cm, 11.4 cm, and 14.7 cm, respectively. Determine the perimeter of the fourth shape.
Péta composed several planar shapes from mutually congruent triangles. The circumferences of the first three are 8 cm, 11.4 cm, and 14.7 cm, respectively. Determine the perimeter of the fourth shape. - Gift baskets
 Alessia and Alexia made some gift baskets to sell. 2/5 of them were Yu-Gi-oh themed, and the rest were Barbie-themed. They sold 3/4 of the yu-gi-oh-themed baskets and 7/12 of the Barbie-themed baskets. They remained with 56 gift baskets. How many gift bas
Alessia and Alexia made some gift baskets to sell. 2/5 of them were Yu-Gi-oh themed, and the rest were Barbie-themed. They sold 3/4 of the yu-gi-oh-themed baskets and 7/12 of the Barbie-themed baskets. They remained with 56 gift baskets. How many gift bas - Five couples
 In how many ways can 5 couples arrange themselves in a row if they stay together?
In how many ways can 5 couples arrange themselves in a row if they stay together? - BODMAS rules
 To solve this problem using BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction), we need to arrange the numbers 50,5,1,10,1,10 in a way that results in 222.
To solve this problem using BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction), we need to arrange the numbers 50,5,1,10,1,10 in a way that results in 222. - Circle - analytics geometry
 Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0.
Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0. - Arithmetic progressions.
 Find the sum of all the numbers between 9 and 204, which is exactly divisible by 3.
Find the sum of all the numbers between 9 and 204, which is exactly divisible by 3.
