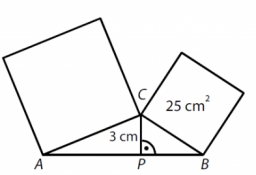
Squares above sides
Two squares are constructed on two sides of the ABC triangle. The square area above the BC side is 25 cm2. The height vc to the side AB is 3 cm long. The heel P of height vc divides the AB side in a 2:1 ratio. The AC side is longer than the BC side. Calculate the length of the AB side in cm.
Calculate the area of the square above the AC side in cm2.
Calculate the area of the square above the AC side in cm2.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- planimetrics
- Pythagorean theorem
- right triangle
- area of a shape
- triangle
- square
- The right triangle altitude theorem
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- A park on map
 A park has an area of ⅙ mi². On a map, the park has an area of 1 ¼ cm². On the map, how many square centimeters represent 1 mi²?
A park has an area of ⅙ mi². On a map, the park has an area of 1 ¼ cm². On the map, how many square centimeters represent 1 mi²? - The rectangle 7
 The rectangle shown has a length (l) of 8 and a width (w) of 6.2. A second rectangle has a length of l + 2.5 and a width of w - 1.4. Find the area of the SECOND rectangle.
The rectangle shown has a length (l) of 8 and a width (w) of 6.2. A second rectangle has a length of l + 2.5 and a width of w - 1.4. Find the area of the SECOND rectangle. - A room
 A room is 8 2/3 m by 5 1/4 m. What is the area of the room?
A room is 8 2/3 m by 5 1/4 m. What is the area of the room? - Height of the box
 The box needs to have a volume of 108 ¾ cubic inches. If the width of the box is going to be 7 ¼ inches, and depth of the box is going to be 1 ¼ inches, what must the height of the box be?
The box needs to have a volume of 108 ¾ cubic inches. If the width of the box is going to be 7 ¼ inches, and depth of the box is going to be 1 ¼ inches, what must the height of the box be? - Ice cream company
 An ice cream company is going to open new stores in Los Angeles, New York, and Orlando. The monthly cost for a square foot of rental space in each city is as follows. town; cost/ft² Los Angeles ; $5.25 New York ; $7.25 Orlando ; $4.25 The store in Los Ang
An ice cream company is going to open new stores in Los Angeles, New York, and Orlando. The monthly cost for a square foot of rental space in each city is as follows. town; cost/ft² Los Angeles ; $5.25 New York ; $7.25 Orlando ; $4.25 The store in Los Ang - Dimensions 83176
 If we reduce the length of the rectangle by 2 cm and the width by 1 cm, its area will decrease by 8 cm². If we increase the length of the rectangle by 1 cm and the width by 2 cm, then its content will increase by 13 cm². What were the original dimensions
If we reduce the length of the rectangle by 2 cm and the width by 1 cm, its area will decrease by 8 cm². If we increase the length of the rectangle by 1 cm and the width by 2 cm, then its content will increase by 13 cm². What were the original dimensions - The capacitor
 The parallel square plates of a 4.5µF Teflon capacitor are 3.2 mm apart. What is the area of the plate?
The parallel square plates of a 4.5µF Teflon capacitor are 3.2 mm apart. What is the area of the plate? - A model
 A model of a house is built on a base that measures 7 3/4 inches wide and 9 1/5 inches long. What is the area of the model house based?
A model of a house is built on a base that measures 7 3/4 inches wide and 9 1/5 inches long. What is the area of the model house based? - A rectangle 13
 A rectangle has an area of 15 square inches. What is the missing side length if one side length is 1 2/3 inches wide?
A rectangle has an area of 15 square inches. What is the missing side length if one side length is 1 2/3 inches wide? - Trim the bushes
 Mason is always helping him to trim the bushes. The area A had a length of 14 m and a breadth of 7 m, and if we are going to combine A and B, the equal is 215 m². The question is: what is the area of B?
Mason is always helping him to trim the bushes. The area A had a length of 14 m and a breadth of 7 m, and if we are going to combine A and B, the equal is 215 m². The question is: what is the area of B? - ET inscribed circle
 An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region.
An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region. - Harold
 Harold made a rectangular dog run in his backyard. The area of the dog run is 96 square feet. What are three different possible dimensions of dog run?
Harold made a rectangular dog run in his backyard. The area of the dog run is 96 square feet. What are three different possible dimensions of dog run? - The triangle 6
 The triangle has an area of 7 ⅞ cm² and a base of 5 ¼ cm. What is the length of h? Explain your reasoning.
The triangle has an area of 7 ⅞ cm² and a base of 5 ¼ cm. What is the length of h? Explain your reasoning. - A concert venue
 The floor of a concert venue is 100 3/4 feet by 75 1/2 feet. What is the area of the floor?
The floor of a concert venue is 100 3/4 feet by 75 1/2 feet. What is the area of the floor? - A farmer 9
 A farmer has 3 hectares of an orchard. ½ of the land is occupied by apples, ⅙ of the remainder is occupied by lemon trees, and tree tomatoes occupy the rest of it. Find the fraction of the land occupied by tree tomatoes.
A farmer has 3 hectares of an orchard. ½ of the land is occupied by apples, ⅙ of the remainder is occupied by lemon trees, and tree tomatoes occupy the rest of it. Find the fraction of the land occupied by tree tomatoes. - Geometric Solid
 A concrete pipe is 1.0 m long. Its inside and outside diameters are 60 cm and 75 cm, respectively. What is the volume of the concrete (cubic meters) needed to make 25 pcs of pipe?
A concrete pipe is 1.0 m long. Its inside and outside diameters are 60 cm and 75 cm, respectively. What is the volume of the concrete (cubic meters) needed to make 25 pcs of pipe? - The bedroom
 The area of the rectangular bedroom is 136 5/8 square feet. If its width is 12 3/4 feet, find its length in simplest form.
The area of the rectangular bedroom is 136 5/8 square feet. If its width is 12 3/4 feet, find its length in simplest form.
