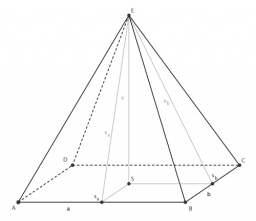
The quadrilateral pyramid
The quadrilateral pyramid has a rectangular base of 24 cm x 3.2dm and a body height of 0.4m. Calculate its volume and surface area.
Correct answer:
Tips for related online calculators
See also our right triangle calculator.
Do you want to convert length units?
Do you know the volume and unit volume, and want to convert volume units?
See also our trigonometric triangle calculator.
Do you want to convert length units?
Do you know the volume and unit volume, and want to convert volume units?
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Right-angled 66364
 From a rectangular board with 2 m and 3 m dimensions, we cut isosceles and right-angled triangles at the corners with an overhang of 40 cm. Calculate the ratio of the rest of the board's areas to its total original area.
From a rectangular board with 2 m and 3 m dimensions, we cut isosceles and right-angled triangles at the corners with an overhang of 40 cm. Calculate the ratio of the rest of the board's areas to its total original area. - Rectangular 63094
 Calculate the perimeter and the area of a rectangular garden if the diagonal length is 18 m long and one of the sides of the garden is 9m long.
Calculate the perimeter and the area of a rectangular garden if the diagonal length is 18 m long and one of the sides of the garden is 9m long. - Rectangle 49153
 Rectangle ABCD, whose | AB | = 5cm, | AC | = 8 cm, ∢ | CAB | = 30 °. How long is the other party, and what is its area?
Rectangle ABCD, whose | AB | = 5cm, | AC | = 8 cm, ∢ | CAB | = 30 °. How long is the other party, and what is its area? - A rectangle 5
 A rectangle has sides of 10 cm and 14 cm. Calculate the angle between a diagonal and a long side.
A rectangle has sides of 10 cm and 14 cm. Calculate the angle between a diagonal and a long side. - Joanne
 Joanne and Roger are planting a rectangular garden. The garden is 8 1/2 ft by 13 ft. They want to use half of the garden for cucumbers and half for tomatoes. They decide to separate the garden into two right triangles. What is the area of the tomato part
Joanne and Roger are planting a rectangular garden. The garden is 8 1/2 ft by 13 ft. They want to use half of the garden for cucumbers and half for tomatoes. They decide to separate the garden into two right triangles. What is the area of the tomato part - Triangular land
 Jana has a rectangular garden measuring 30 meters by 72 meters that she wants to split diagonally from corner to corner using a fence. How long does her fence need to be?
Jana has a rectangular garden measuring 30 meters by 72 meters that she wants to split diagonally from corner to corner using a fence. How long does her fence need to be? - Angle of diagonals
 Calculate a rectangle's perimeter and area if its diagonal is 14 cm and the diagonals form an angle of 130°.
Calculate a rectangle's perimeter and area if its diagonal is 14 cm and the diagonals form an angle of 130°. - Side and diagonal
 Find the circumference and the area of the rectangle if given: side a = 8 cm diagonal u = 10 cm.
Find the circumference and the area of the rectangle if given: side a = 8 cm diagonal u = 10 cm. - Metal washers
 Metal washers with a diameter of 80 mm are cut from a strip of steel sheet with a width of 10 cm and a length of 2 m. When two adjacent circles meet, calculate the material waste percentage if no material is lost.
Metal washers with a diameter of 80 mm are cut from a strip of steel sheet with a width of 10 cm and a length of 2 m. When two adjacent circles meet, calculate the material waste percentage if no material is lost. - Quadrilateral pyramid,
 A quadrilateral pyramid has a rectangular base with 24 cm and 13 cm dimensions. The height of the pyramid is 18cm. Calculate 1/the area of the base 2/casing area 3/pyramid surface 4/volume of the pyramid
A quadrilateral pyramid has a rectangular base with 24 cm and 13 cm dimensions. The height of the pyramid is 18cm. Calculate 1/the area of the base 2/casing area 3/pyramid surface 4/volume of the pyramid - Perimeter and diagonal
 The perimeter of the rectangle is 82 m, and the length of its diagonal is 29 m. Find the dimensions of the rectangle.
The perimeter of the rectangle is 82 m, and the length of its diagonal is 29 m. Find the dimensions of the rectangle. - Quadrilateral pyramid
 Calculate the surface of a quadrilateral pyramid, which has a rectangular base with dimensions a = 8 cm, b = 6 cm, and height H = 10 cm.
Calculate the surface of a quadrilateral pyramid, which has a rectangular base with dimensions a = 8 cm, b = 6 cm, and height H = 10 cm. - Triangular prism
 Calculate the surface of a regular triangular prism; the base's edges are 6 cm long, and the height of the prism is 15 cm.
Calculate the surface of a regular triangular prism; the base's edges are 6 cm long, and the height of the prism is 15 cm. - Height of the cuboid
 Cuboid with a rectangular base, measuring 3 cm and 4 cm diagonal, has a body 13 centimeters long. What is the height of the cuboid?
Cuboid with a rectangular base, measuring 3 cm and 4 cm diagonal, has a body 13 centimeters long. What is the height of the cuboid? - The pyramid 4s
 The pyramid with a rectangular base measuring 6 dm and 8 dm has a side edge of a length of 13 dm. Calculate the surface area and volume of this pyramid.
The pyramid with a rectangular base measuring 6 dm and 8 dm has a side edge of a length of 13 dm. Calculate the surface area and volume of this pyramid. - Rectangular base pyramid
 The pyramid has a rectangular base of 2.8 m and 1.4 m and a height of 2.5 meters. Calculate an area of the shell of the pyramid.
The pyramid has a rectangular base of 2.8 m and 1.4 m and a height of 2.5 meters. Calculate an area of the shell of the pyramid. - A rectangle 2
 A rectangle has a diagonal length of 74cm. Its side lengths are in a ratio of 5:3. Find its side lengths.
A rectangle has a diagonal length of 74cm. Its side lengths are in a ratio of 5:3. Find its side lengths.
