Suppose
Suppose you know that the length of a line segment is 15, x2=6, y2=14, and x1= -3. Find the possible value of y1. Is there more than one possible answer? Why or why not?
Correct answer:
Showing 1 comment:
Matematik
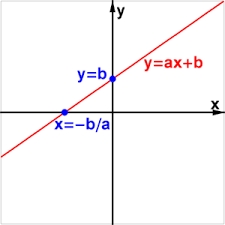
we make circle k with centre S(x2,y2) and radius r = 15 . Then we make vertical line x= -3 . It make two intersections with circle k thus solutions are two: y11,y12.
Tips for related online calculators
The line slope calculator is helpful for basic calculations in analytic geometry. The coordinates of two points in the plane calculate slope, normal and parametric line equation(s), slope, directional angle, direction vector, the length of the segment, intersections of the coordinate axes, etc.
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Do you want to convert length units?
The Pythagorean theorem is the base for the right triangle calculator.
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Do you want to convert length units?
The Pythagorean theorem is the base for the right triangle calculator.
You need to know the following knowledge to solve this word math problem:
- geometry
- analytic geometry
- line
- algebra
- quadratic equation
- equation
- arithmetic
- square root
- square (second power, quadratic)
- absolute value
- planimetrics
- Pythagorean theorem
- circle
- square
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Human population
 The populations of two cities after t years can be modeled by -150t+50,000 and 50t+75,000. What is the difference in the populations of the towns when t=4?
The populations of two cities after t years can be modeled by -150t+50,000 and 50t+75,000. What is the difference in the populations of the towns when t=4? - The midday
 The midday temperature in Pensacola Beach was 84°F. For the next five hours, it changed to –2°F per hour. The expression 84 − |−2 ⋅ 5| represents the current temperature. What is the current temperature in degrees Fahrenheit?
The midday temperature in Pensacola Beach was 84°F. For the next five hours, it changed to –2°F per hour. The expression 84 − |−2 ⋅ 5| represents the current temperature. What is the current temperature in degrees Fahrenheit? - A teacher 3
 A teacher gives pens and pencils to elementary students at an equal rate in each classroom. Pencils; Pens 18 ; 72 29 ; A 35 ; 140 B ; 168 Determine the missing value for the letter B.
A teacher gives pens and pencils to elementary students at an equal rate in each classroom. Pencils; Pens 18 ; 72 29 ; A 35 ; 140 B ; 168 Determine the missing value for the letter B. - Proportional relationship 3
 Which table below shows a proportional relationship? A. x ; y 3; 12 4; 16 5; 20 6; 24 7; 28 B. x ; y 3; 15 4; 20 5; 25 6; 35 7; 40 C. x ; y 3; 24 4; 32 5; 45 6; 48 7; 56 D. x ; y 3 ; 21 4; 24 5; 35 6; 42 7; 49
Which table below shows a proportional relationship? A. x ; y 3; 12 4; 16 5; 20 6; 24 7; 28 B. x ; y 3; 15 4; 20 5; 25 6; 35 7; 40 C. x ; y 3; 24 4; 32 5; 45 6; 48 7; 56 D. x ; y 3 ; 21 4; 24 5; 35 6; 42 7; 49
- Collinear lines
 Points A, B, and C are collinear, and B lies between A and C. If AC = 48, AB = 2x + 2, and BC = 3x + 6, what is BC?
Points A, B, and C are collinear, and B lies between A and C. If AC = 48, AB = 2x + 2, and BC = 3x + 6, what is BC? - The tangent of the hyperbola
 Write the equation of the tangent of the hyperbola 9x²−4y²=36 at the point T =[t1,4].
Write the equation of the tangent of the hyperbola 9x²−4y²=36 at the point T =[t1,4]. - There 35
 There are three points on a straight line: A, BC. If CD = 8x, DE = 3, and CE = x + 10, what is CD? Simplify your answer and write it as a proper fraction, mixed number, or integer.
There are three points on a straight line: A, BC. If CD = 8x, DE = 3, and CE = x + 10, what is CD? Simplify your answer and write it as a proper fraction, mixed number, or integer. - X intercept
 Given: 3y+2x=-6 Calculate the X-intercept.
Given: 3y+2x=-6 Calculate the X-intercept. - Line equation:
 Line equation: y-3=8/9(x-5) Solve for slope
Line equation: y-3=8/9(x-5) Solve for slope
- Y-intercept 2
 What is the y-intercept of 4x + 8y =16? Write coordinates of x0, y0 of that y-intercept.
What is the y-intercept of 4x + 8y =16? Write coordinates of x0, y0 of that y-intercept. - Slope of the line
 What is the slope of the line passing through two points (-3,5) and (2, -1)
What is the slope of the line passing through two points (-3,5) and (2, -1) - A function
 A function follows the rule "y is 3 less than half of x". Express y as a function of x in the form of an equation.
A function follows the rule "y is 3 less than half of x". Express y as a function of x in the form of an equation. - Y-intercept
 Find the y-intercept of the graph (-3,-3), (4,3), (8,3). The x-intercept is 1/2.
Find the y-intercept of the graph (-3,-3), (4,3), (8,3). The x-intercept is 1/2. - Line in normal form
 Try to find the equation of a line given two points in the form Ax+By=C. passes through the points: (2,1) and (-2,2)
Try to find the equation of a line given two points in the form Ax+By=C. passes through the points: (2,1) and (-2,2)
- Line slope
 What is the slope of the line with points (-1,-3) and (-5, 2)?
What is the slope of the line with points (-1,-3) and (-5, 2)? - The slope 2
 What is the slope of the line that passes through the points (-4, -7) and (-2,-19)? Write your answer in the simplest form.
What is the slope of the line that passes through the points (-4, -7) and (-2,-19)? Write your answer in the simplest form. - Temperature - linear function
 In the morning, at 08:00 hours, the temperature was -8°C, and in the afternoon, at 16:00 hours, the temperature was 24°C. Assuming that the temperature changes steadily, what was the temperature at 1300 hours, and what was the time when the temperature wa
In the morning, at 08:00 hours, the temperature was -8°C, and in the afternoon, at 16:00 hours, the temperature was 24°C. Assuming that the temperature changes steadily, what was the temperature at 1300 hours, and what was the time when the temperature wa
