Water container
The cube-shaped container is filled to two-thirds of its height. If we pour 18 liters, it will be filled to three-fifths of the height. What is the volume of the whole container?
Correct answer:

Tips for related online calculators
Need help calculating sum, simplifying, or multiplying fractions? Try our fraction calculator.
Check out our ratio calculator.
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Tip: Our volume units converter will help you convert volume units.
Check out our ratio calculator.
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
- algebra
- equation
- expression of a variable from the formula
- solid geometry
- cube
- basic functions
- ratio
- numbers
- fractions
Units of physical quantities:
Related math problems and questions:
- Wooden 4283
 Alex cut the wooden block into two parts in one cut. Which body could he not get?
Alex cut the wooden block into two parts in one cut. Which body could he not get? - Tent - spherical cap
 I have a tent in the shape of a spherical cap. Assume we want the volume to be 4 cubic meters, to sleep two or three people. Assume that the material making up the dome of the ten is twice as expensive per square as the material touching the ground. What
I have a tent in the shape of a spherical cap. Assume we want the volume to be 4 cubic meters, to sleep two or three people. Assume that the material making up the dome of the ten is twice as expensive per square as the material touching the ground. What - Storage shed
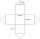 Frank designed a net for a storage shed that he is going to construct out of metal. The design consists of a square base and four square sides, plus four triangular parts that make up the roof. A square base of 6 feet and four square sides, plus 4 feet of
Frank designed a net for a storage shed that he is going to construct out of metal. The design consists of a square base and four square sides, plus four triangular parts that make up the roof. A square base of 6 feet and four square sides, plus 4 feet of - Quadrilateral 70294
 The edge lengths of a quadrilateral prism are in the ratio a: b: c = 2:4:5. The surface of the prism is 57 cm². Calculate the volume.
The edge lengths of a quadrilateral prism are in the ratio a: b: c = 2:4:5. The surface of the prism is 57 cm². Calculate the volume. - Side wall planes
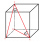 Find the volume and surface of a cuboid whose side c is 30 cm long and the body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls.
Find the volume and surface of a cuboid whose side c is 30 cm long and the body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls. - Sphere submerged in the cone
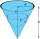 A right circular cone with a top width of 24 cm and an altitude of 8 cm is filled with water. A spherical steel ball with a radius of 3.0cm is submerged in the cone. Find the volume of water below the sphere.
A right circular cone with a top width of 24 cm and an altitude of 8 cm is filled with water. A spherical steel ball with a radius of 3.0cm is submerged in the cone. Find the volume of water below the sphere. - Quadrilateral 58663
 They melted the steel part in the shape of a truncated quadrilateral needle and produced three identical cubes. Determine the surface area of one cube if the edges of the bases of the pyramid are 30 mm and 80 mm and the pyramid's height is 60 mm. I don't
They melted the steel part in the shape of a truncated quadrilateral needle and produced three identical cubes. Determine the surface area of one cube if the edges of the bases of the pyramid are 30 mm and 80 mm and the pyramid's height is 60 mm. I don't - Regular square prism
 The volume of a regular square prism is 192 cm³. The size of its base edge and the body height is 1:3. Calculate the surface of the prism.
The volume of a regular square prism is 192 cm³. The size of its base edge and the body height is 1:3. Calculate the surface of the prism. - Two hemispheres
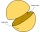 In a wooden hemisphere with a radius r = 1, the carpenter created a hemispherical depression with a radius r/2. The bases of both hemispheres lie in the same plane. What is the surface of the created body (including the surface of the depression)?
In a wooden hemisphere with a radius r = 1, the carpenter created a hemispherical depression with a radius r/2. The bases of both hemispheres lie in the same plane. What is the surface of the created body (including the surface of the depression)? - Hemisphere cut
 Calculate the spherical layer's volume that remains from the hemisphere after the 3 cm section is cut. The height of the hemisphere is 10 cm.
Calculate the spherical layer's volume that remains from the hemisphere after the 3 cm section is cut. The height of the hemisphere is 10 cm. - Quadrilateral prism
 Calculate the volume (V) and the surface (S) of a regular quadrilateral prism whose height is 28.6 cm and the deviation of the body diagonal from the base plane is 50°.
Calculate the volume (V) and the surface (S) of a regular quadrilateral prism whose height is 28.6 cm and the deviation of the body diagonal from the base plane is 50°. - Hemisphere - roof
 The shape of the observatory dome is close to the hemisphere. Its outer diameter is 11 m. How many kilograms of paint and how many liters of thinner are used for its double coat if you know that 1 kg of paint diluted with 1 deciliter of thinner will paint
The shape of the observatory dome is close to the hemisphere. Its outer diameter is 11 m. How many kilograms of paint and how many liters of thinner are used for its double coat if you know that 1 kg of paint diluted with 1 deciliter of thinner will paint - Wooden container
 The locksmith should cover the cube-shaped wooden container with a metal sheet inside. The outer edge of the container is 54cm. The wall thickness is 25 mm. The container has no lid. Calculate. How many sheets will be needed to cover it?
The locksmith should cover the cube-shaped wooden container with a metal sheet inside. The outer edge of the container is 54cm. The wall thickness is 25 mm. The container has no lid. Calculate. How many sheets will be needed to cover it? - Spherical cap
 Place a part of the sphere on a 4.6 cm cylinder so that the surface of this section is 20 cm². Determine the radius r of the sphere from which we cut the spherical cap.
Place a part of the sphere on a 4.6 cm cylinder so that the surface of this section is 20 cm². Determine the radius r of the sphere from which we cut the spherical cap. - The observatory
 The dome of the hemisphere-shaped observatory is 5.4 meters high. How many square meters of sheet metal need to be covered to cover it, and must we add 15 percent to the minimum amount due to joints and waste?
The dome of the hemisphere-shaped observatory is 5.4 meters high. How many square meters of sheet metal need to be covered to cover it, and must we add 15 percent to the minimum amount due to joints and waste? - Hemispherical hollow
 The vessel's hemispherical hollow is filled with water to a height of 10 cm =. How many liters of water are inside if the hollow's inside diameter is d = 28cm?
The vessel's hemispherical hollow is filled with water to a height of 10 cm =. How many liters of water are inside if the hollow's inside diameter is d = 28cm? - Surface of cubes
 Peter molded a cuboid of 2 cm, 4cm, and 9cm of plasticine. Then the plasticine was split into two parts in a ratio of 1:8. From each piece made, a cube. In what ratio are the surfaces of these cubes?
Peter molded a cuboid of 2 cm, 4cm, and 9cm of plasticine. Then the plasticine was split into two parts in a ratio of 1:8. From each piece made, a cube. In what ratio are the surfaces of these cubes?
