Surface area
The volume of a cone is 1000 cm3, and the area of the axis cut is 100 cm2. Calculate the surface area of the cone.
Correct answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Tent - spherical cap
 I have a tent in the shape of a spherical cap. Assume we want the volume to be 4 cubic meters, to sleep two or three people. Assume that the material making up the dome of the ten is twice as expensive per square as the material touching the ground. What
I have a tent in the shape of a spherical cap. Assume we want the volume to be 4 cubic meters, to sleep two or three people. Assume that the material making up the dome of the ten is twice as expensive per square as the material touching the ground. What - A cone 3
 A cone has a diameter of x cm and a slant height of y cm. A square pyramid has a base side length of x cm and a slant height of y cm. Which has the greater surface area? Explain.
A cone has a diameter of x cm and a slant height of y cm. A square pyramid has a base side length of x cm and a slant height of y cm. Which has the greater surface area? Explain. - The perimeter
 The perimeter of the base of a regular quadrilateral pyramid is the same as its height. The pyramid has a volume of 288 dm³. Calculate its surface area round the result to the whole dm².
The perimeter of the base of a regular quadrilateral pyramid is the same as its height. The pyramid has a volume of 288 dm³. Calculate its surface area round the result to the whole dm². - A Pile of salt
 A Pile of salt has been stored in the shape of a cone. Mr. Terwilliker knows that the pile is 20 feet tall and 102 feet in circumference at the base. What area of the conical tarpaulin (a large sheet of material) is needed to cover the pile?
A Pile of salt has been stored in the shape of a cone. Mr. Terwilliker knows that the pile is 20 feet tall and 102 feet in circumference at the base. What area of the conical tarpaulin (a large sheet of material) is needed to cover the pile? - A cone 2
 A cone has a slant height of 10 cm and a square curved surface area of 50 pi cm. Find the base radius of the cone.
A cone has a slant height of 10 cm and a square curved surface area of 50 pi cm. Find the base radius of the cone. - Calculate 73704
 A vertical regular 3-sided pyramid is given. The side of the base a = 5cm, and the height is 8 cm. Calculate the volume and area.
A vertical regular 3-sided pyramid is given. The side of the base a = 5cm, and the height is 8 cm. Calculate the volume and area. - Cylinder-shaped 71384
 My father installed a cylinder-shaped pool in the garden with a bottom diameter of 6 m and a height of 1.5 m. how many hectoliters of water can fit in the pool? How many m² of space must be cleaned after draining the pool?
My father installed a cylinder-shaped pool in the garden with a bottom diameter of 6 m and a height of 1.5 m. how many hectoliters of water can fit in the pool? How many m² of space must be cleaned after draining the pool? - Deviation 70434
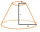 Frustum has the base radii of the figures r1 and r2: r1> r2, r2 = s, and if the side deviation from the base plane is 60°. Express the surface and volume of the cone frustum using its side s.
Frustum has the base radii of the figures r1 and r2: r1> r2, r2 = s, and if the side deviation from the base plane is 60°. Express the surface and volume of the cone frustum using its side s. - Quadrilateral 70294
 The edge lengths of a quadrilateral prism are in the ratio a: b: c = 2:4:5. The surface of the prism is 57 cm². Calculate the volume.
The edge lengths of a quadrilateral prism are in the ratio a: b: c = 2:4:5. The surface of the prism is 57 cm². Calculate the volume. - Slant height 2
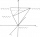 A regular triangular pyramid with a slant height of 9 m has a volume of 50 m³. Find the lateral area of the pyramid.
A regular triangular pyramid with a slant height of 9 m has a volume of 50 m³. Find the lateral area of the pyramid. - Base side
 In a quadrilateral prism, are known surface area S = 12400 mm2, base side m = 40mm, and prism height = 120mm. What is the length of base side n =?
In a quadrilateral prism, are known surface area S = 12400 mm2, base side m = 40mm, and prism height = 120mm. What is the length of base side n =? - The surface
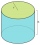 The surface of the cylinder is 1570 cm²; its height is 15 cm. Find the volume and radius of the base.
The surface of the cylinder is 1570 cm²; its height is 15 cm. Find the volume and radius of the base. - How to
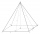 How to find a total surface of a rectangular pyramid if each face is 8 dm high and the base is 10 dm by 6 dm?
How to find a total surface of a rectangular pyramid if each face is 8 dm high and the base is 10 dm by 6 dm? - Frustrum - volume, area
 Calculate the surface and volume of the truncated cone. The radius of the smaller figure is 4 cm, the height of the cone is 4 cm, and the side of the truncated cone is 5 cm.
Calculate the surface and volume of the truncated cone. The radius of the smaller figure is 4 cm, the height of the cone is 4 cm, and the side of the truncated cone is 5 cm. - Regular quadrilateral pyramid
 Find the surface area of a regular quadrilateral pyramid if for its volume V and body height v and the base edge a applies: V = 2.8 m³, v = 2.1 m
Find the surface area of a regular quadrilateral pyramid if for its volume V and body height v and the base edge a applies: V = 2.8 m³, v = 2.1 m - Regular square prism
 The volume of a regular square prism is 192 cm³. The size of its base edge and the body height is 1:3. Calculate the surface of the prism.
The volume of a regular square prism is 192 cm³. The size of its base edge and the body height is 1:3. Calculate the surface of the prism. - Determine 46401
 The volume of the sphere is 20% larger than the volume of the cone. Find its surface if the volume of the cone is 320 cm³.
The volume of the sphere is 20% larger than the volume of the cone. Find its surface if the volume of the cone is 320 cm³.
