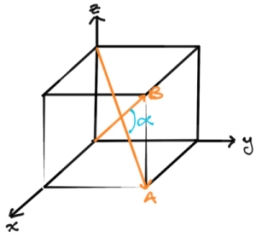
Angle of the body diagonals
Using the vector dot product calculate the angle of the body diagonals of the cube.
Correct answer:
Tips for related online calculators
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- geometry
- analytic geometry
- vector
- scalar product
- arithmetic
- absolute value
- solid geometry
- cube
- space diagonal
- planimetrics
- Pythagorean theorem
- right triangle
- triangle
- goniometry and trigonometry
- cosine
- arccosine
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Matrices 2
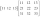 Suppose A=(1 6 3 −2) B=(4 −3 −4 3) find 2A+3B
Suppose A=(1 6 3 −2) B=(4 −3 −4 3) find 2A+3B - Book Store
 The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w
The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w - Vectors
 Find the magnitude of the angle between two vectors u = (3; -5) and v = (10; 6)
Find the magnitude of the angle between two vectors u = (3; -5) and v = (10; 6) - Space vectors 3D
 The vectors u = (1; 3; -4), v = (0; 1; 1) are given. Find the size of these vectors, calculate the angle of the vectors, and the distance between the vectors.
The vectors u = (1; 3; -4), v = (0; 1; 1) are given. Find the size of these vectors, calculate the angle of the vectors, and the distance between the vectors.
- Perpendicular projection
 Determine the distance of a point B[1, -3] from the perpendicular projection of a point A[3, -2] on a straight line 2 x + y + 1 = 0.
Determine the distance of a point B[1, -3] from the perpendicular projection of a point A[3, -2] on a straight line 2 x + y + 1 = 0. - Direction vector
 The line p is given by the point P [- 0,5; 1] and the direction vector s = (1,5; - 3) determines: A) value of parameter t for points X [- 1,5; 3], Y [1; - 2] lines p B) whether the points R [0,5; - 1], S [1,5; 3] lies on the line p C) parametric equations
The line p is given by the point P [- 0,5; 1] and the direction vector s = (1,5; - 3) determines: A) value of parameter t for points X [- 1,5; 3], Y [1; - 2] lines p B) whether the points R [0,5; - 1], S [1,5; 3] lies on the line p C) parametric equations - Vector v4
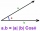 Find the vector v4 perpendicular to the vectors v1 = (1, 1, 1, -1), v2 = (1, 1, -1, 1) and v3 = (0, 0, 1, 1)
Find the vector v4 perpendicular to the vectors v1 = (1, 1, 1, -1), v2 = (1, 1, -1, 1) and v3 = (0, 0, 1, 1) - Decide 2
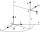 Decide whether points A[-2, -5], B[4, 3], and C[16, -1] lie on the same line
Decide whether points A[-2, -5], B[4, 3], and C[16, -1] lie on the same line - Vector perpendicular
 Find the vector a = (2, y, z) so that a⊥ b and a ⊥ c where b = (-1, 4, 2) and c = (3, -3, -1)
Find the vector a = (2, y, z) so that a⊥ b and a ⊥ c where b = (-1, 4, 2) and c = (3, -3, -1)
- Vector equation
 Let’s v = (1, 2, 1), u = (0, -1, 3) and w = (1, 0, 7) . Solve the vector equation c1 v + c2 u + c3 w = 0 for variables c1 c2, c3 and decide weather v, u and w are linear dependent or independent
Let’s v = (1, 2, 1), u = (0, -1, 3) and w = (1, 0, 7) . Solve the vector equation c1 v + c2 u + c3 w = 0 for variables c1 c2, c3 and decide weather v, u and w are linear dependent or independent - Parallel and orthogonal
 I need math help in this problem: a=(-5, 5 3) b=(-2,-4,-5) (they are vectors) Decompose the vector b into b=v+w where v is parallel to a and w is orthogonal to a, find v and w
I need math help in this problem: a=(-5, 5 3) b=(-2,-4,-5) (they are vectors) Decompose the vector b into b=v+w where v is parallel to a and w is orthogonal to a, find v and w - Parametric form
 Calculate the distance of point A [2,1] from the line p: X = -1 + 3 t Y = 5-4 t Line p has a parametric form of the line equation.
Calculate the distance of point A [2,1] from the line p: X = -1 + 3 t Y = 5-4 t Line p has a parametric form of the line equation. - Perpendicular and parallel
 Find the value of t if 2tx+5y-6=0 and 5x-4y+8=0 are perpendicular and parallel lines. What angle does each line make with the x-axis, and find the angle between the lines?
Find the value of t if 2tx+5y-6=0 and 5x-4y+8=0 are perpendicular and parallel lines. What angle does each line make with the x-axis, and find the angle between the lines? - Coordinates of square vertices
 The ABCD square has the center S [−3, −2] and the vertex A [1, −3]. Find the coordinates of the other vertices of the square.
The ABCD square has the center S [−3, −2] and the vertex A [1, −3]. Find the coordinates of the other vertices of the square.
- Scalar product
 Calculate the scalar product of two vectors: (2.5) (-1, -4)
Calculate the scalar product of two vectors: (2.5) (-1, -4) - Equation of the circle
 Find the equation of the circle with the center at (1,20), which touches the line 8x+5y-19=0
Find the equation of the circle with the center at (1,20), which touches the line 8x+5y-19=0 - Three points 2
 The three points are A(3, 8), B(6, 2), and C(10, 2). Point D is such that the line DA is perpendicular to AB, and DC is parallel to AB. Calculate the coordinates of D.
The three points are A(3, 8), B(6, 2), and C(10, 2). Point D is such that the line DA is perpendicular to AB, and DC is parallel to AB. Calculate the coordinates of D.
