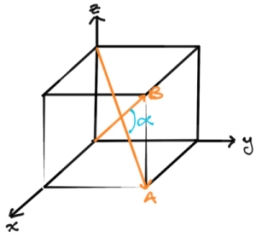
Angle of the body diagonals
Using the vector dot product calculate the angle of the body diagonals of the cube.
Correct answer:
Tips for related online calculators
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- geometry
- analytic geometry
- vector
- scalar product
- arithmetic
- absolute value
- solid geometry
- cube
- space diagonal
- planimetrics
- Pythagorean theorem
- right triangle
- triangle
- goniometry and trigonometry
- cosine
- arccosine
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Ratio iso triangle
 The ratio of the sides of an isosceles triangle is 7:6:7. Find the base angle to the nearest answer correct to 3 significant figures.
The ratio of the sides of an isosceles triangle is 7:6:7. Find the base angle to the nearest answer correct to 3 significant figures. - Trapezoid MO
 The rectangular trapezoid ABCD with the right angle at point B, |AC| = 12, |CD| = 8, diagonals are perpendicular to each other. Calculate the perimeter and area of the trapezoid.
The rectangular trapezoid ABCD with the right angle at point B, |AC| = 12, |CD| = 8, diagonals are perpendicular to each other. Calculate the perimeter and area of the trapezoid. - Three pillars
 On a straight road, three pillars are 6 m high at the same distance of 10 m. At what angle of view does Vlado see each pillar if it is 30 m from the first and his eyes are 1.8 m high?
On a straight road, three pillars are 6 m high at the same distance of 10 m. At what angle of view does Vlado see each pillar if it is 30 m from the first and his eyes are 1.8 m high? - Subtract polar forms
 Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form
Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form - Let z 2
 Let z = 2 - sqrt(3i). Find z6 and express your answer in rectangular form. if z = 2 - 2sqrt(3 i) then r = |z| = sqrt(2 ^ 2 + (- 2sqrt(3)) ^ 2) = sqrt(16) = 4 and theta = tan -2√3/2=-π/3
Let z = 2 - sqrt(3i). Find z6 and express your answer in rectangular form. if z = 2 - 2sqrt(3 i) then r = |z| = sqrt(2 ^ 2 + (- 2sqrt(3)) ^ 2) = sqrt(16) = 4 and theta = tan -2√3/2=-π/3 - In the desert
 A man wondering in the desert walks 5.7 miles in the direction S 26° W. He then turns 90° and walks 9 miles in the direction N 49° W. At that time, how far is he from his starting point, and what is his bearing from his starting point?
A man wondering in the desert walks 5.7 miles in the direction S 26° W. He then turns 90° and walks 9 miles in the direction N 49° W. At that time, how far is he from his starting point, and what is his bearing from his starting point? - Crosswind
 A plane is traveling 45 degrees N of E at 320 km/h when it comes across a current from S of E at 115 degrees of 20 km/h. What are the airplane's new course and speed?
A plane is traveling 45 degrees N of E at 320 km/h when it comes across a current from S of E at 115 degrees of 20 km/h. What are the airplane's new course and speed? - Sin cos tan
 If cos y = 0.8, 0° ≤ y ≤ 90°, find the value of (4 tan y) / (cos y-sin y)
If cos y = 0.8, 0° ≤ y ≤ 90°, find the value of (4 tan y) / (cos y-sin y) - Subtracting complex in polar
 Given w =√2(cosine (pi/4) + i sine (pi/4) ) and z = 2 (cosine (pi/2) + i sine (pi/2) ). What is w - z expressed in polar form?
Given w =√2(cosine (pi/4) + i sine (pi/4) ) and z = 2 (cosine (pi/2) + i sine (pi/2) ). What is w - z expressed in polar form? - The body
 The body slides down an inclined plane, forming an angle α = π / 4 = 45° under the action of a horizontal plane under the effect of friction forces with acceleration a = 2.4 m/s². At what angle β must the plane be inclined so that the body slides on it af
The body slides down an inclined plane, forming an angle α = π / 4 = 45° under the action of a horizontal plane under the effect of friction forces with acceleration a = 2.4 m/s². At what angle β must the plane be inclined so that the body slides on it af - Space diagonal angles
 Calculate the angle between the body diagonal and the side edge c of the block with dimensions: a = 28cm, b = 45cm, and c = 73cm. Then, find the angle between the body diagonal and the plane of the base ABCD.
Calculate the angle between the body diagonal and the side edge c of the block with dimensions: a = 28cm, b = 45cm, and c = 73cm. Then, find the angle between the body diagonal and the plane of the base ABCD. - Triangle in a square
 In a square ABCD with side a = 6 cm, point E is the center of side AB, and point F is the center of side BC. Calculate the size of all angles of the triangle DEF and the lengths of its sides.
In a square ABCD with side a = 6 cm, point E is the center of side AB, and point F is the center of side BC. Calculate the size of all angles of the triangle DEF and the lengths of its sides. - The rescue helicopter
 The rescue helicopter is above the landing site at a height of 180m. The rescue operation site can be seen from here at a depth angle of 52°40'. How far will the helicopter land from the rescue site?
The rescue helicopter is above the landing site at a height of 180m. The rescue operation site can be seen from here at a depth angle of 52°40'. How far will the helicopter land from the rescue site? - Tetrahedral pyramid
 Determine the surface of a regular tetrahedral pyramid when its volume is V = 120 and the angle of the sidewall with the base plane is α = 42° 30'.
Determine the surface of a regular tetrahedral pyramid when its volume is V = 120 and the angle of the sidewall with the base plane is α = 42° 30'. - The aspect ratio
 The aspect ratio of the rectangular triangle is 13:12:5. Calculate the internal angles of the triangle.
The aspect ratio of the rectangular triangle is 13:12:5. Calculate the internal angles of the triangle. - Coordinates of square vertices
 I have coordinates of square vertices A / -3; 1/and B/1; 4 /. Find coordinates of vertices C and D, C and D. Thanks, Peter.
I have coordinates of square vertices A / -3; 1/and B/1; 4 /. Find coordinates of vertices C and D, C and D. Thanks, Peter. - Roof angle
 The house's roof has the shape of an isosceles triangle with arms 4 m long and the size of the base 6 m. How big an angle alpha does its roof make?
The house's roof has the shape of an isosceles triangle with arms 4 m long and the size of the base 6 m. How big an angle alpha does its roof make?
