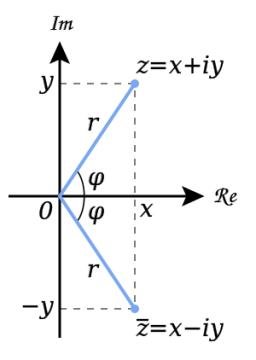
Imaginary numbers
Find two imaginary numbers whose sum is a real number. How are the two imaginary numbers related?
What is their sum?
What is their sum?
Correct answer:
Showing 2 comments:
Tips for related online calculators
Try our complex numbers calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- EE school boarding
 Three vectors, A, B, and C, are related as follows: A/C = 2 at 120 deg, A + B = -5 + j15, C = conjugate of B. Find C.
Three vectors, A, B, and C, are related as follows: A/C = 2 at 120 deg, A + B = -5 + j15, C = conjugate of B. Find C. - Let z 3
 Let z = -5 + i and w = 4 - 2i. Compute z - w and write your final answer in a + bi form. x = z - w
Let z = -5 + i and w = 4 - 2i. Compute z - w and write your final answer in a + bi form. x = z - w - Evaluate complex eq
 If z=x+yi and 3x+(3x-y)i=4-6i then z=
If z=x+yi and 3x+(3x-y)i=4-6i then z= - Subtract polar forms
 Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form
Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form - Complex equation
 If c - d = 2 and c = 12 + 7 i, find d. Write the result in the form of a + bi.
If c - d = 2 and c = 12 + 7 i, find d. Write the result in the form of a + bi. - Suppose 10
 Suppose 4+7i is a solution of 5z2+Az+B=0, where A, B∈R. Find A and B.
Suppose 4+7i is a solution of 5z2+Az+B=0, where A, B∈R. Find A and B. - The expression 2
 The expression (3+i)(1+2i) can be written in the form a+bi, where a and b are integers. What are the values of a and b?
The expression (3+i)(1+2i) can be written in the form a+bi, where a and b are integers. What are the values of a and b? - Conjugate coordinates
 If the rectangular conjugate of the polar vector 12 angle 35 degrees is equal to x+yi, find the sum of x and y.
If the rectangular conjugate of the polar vector 12 angle 35 degrees is equal to x+yi, find the sum of x and y. - Find all 2
 Find all the complex solutions (write the answer in the form x+iy) of the system. {|z-12|/|z-8i|=5/3 ; |z-4|=|z-8|
Find all the complex solutions (write the answer in the form x+iy) of the system. {|z-12|/|z-8i|=5/3 ; |z-4|=|z-8| - Midpoint between conjugate
 Find the midpoint between two roots: 2+3.464i and 2 - 3.464i
Find the midpoint between two roots: 2+3.464i and 2 - 3.464i - Let z 2
 Let z = 2 - sqrt(3i). Find z6 and express your answer in rectangular form. if z = 2 - 2sqrt(3 i) then r = |z| = sqrt(2 ^ 2 + (- 2sqrt(3)) ^ 2) = sqrt(16) = 4 and theta = tan -2√3/2=-π/3
Let z = 2 - sqrt(3i). Find z6 and express your answer in rectangular form. if z = 2 - 2sqrt(3 i) then r = |z| = sqrt(2 ^ 2 + (- 2sqrt(3)) ^ 2) = sqrt(16) = 4 and theta = tan -2√3/2=-π/3 - Alternating circuit
 In an alternating circuit, the total voltage V is given by V=V1 +V2 If V=(12.2+6.8i) V and V1=(7.8-2.5i) V, find the voltage V2.
In an alternating circuit, the total voltage V is given by V=V1 +V2 If V=(12.2+6.8i) V and V1=(7.8-2.5i) V, find the voltage V2. - Complex conjugate
 What is the conjugate of the expression 5√6 + 6√5 i? A.) -5√6 + 6√5 i B.) 5√6 - 6√5 i C.) -5√6 - 6√5 i D.) 6√5 - 5√6i
What is the conjugate of the expression 5√6 + 6√5 i? A.) -5√6 + 6√5 i B.) 5√6 - 6√5 i C.) -5√6 - 6√5 i D.) 6√5 - 5√6i - ABS, ARG, CONJ, RECIPROCAL
 Let z=-√2-√2i where i2 = -1. Find |z|, arg(z), z* (where * indicates the complex conjugate), and (1/z). Where appropriate, write your answers in the form a + i b, where both a and b are real numbers. Indicate the positions of z, z*, and (1/z) on an Argand
Let z=-√2-√2i where i2 = -1. Find |z|, arg(z), z* (where * indicates the complex conjugate), and (1/z). Where appropriate, write your answers in the form a + i b, where both a and b are real numbers. Indicate the positions of z, z*, and (1/z) on an Argand - Suppose 5
 Suppose z5=2+3i and z6=6+9i are complex numbers and 3 z5 + 7 z6= m+in. What is the value of m and n?
Suppose z5=2+3i and z6=6+9i are complex numbers and 3 z5 + 7 z6= m+in. What is the value of m and n? - Complex plane mapping
 Show that the mapping w = z +c/z, where z = x+iy, w = u+iv, and c is a real number, maps the circle |z| = 1 in the z-plane into an ellipse in the (u, v) plane.
Show that the mapping w = z +c/z, where z = x+iy, w = u+iv, and c is a real number, maps the circle |z| = 1 in the z-plane into an ellipse in the (u, v) plane. - Mistake in expression
 While attempting to multiply the expression (2 - 5i)(5 + 2i), a student made a mistake. (2 - 5i)(5 + 2i) = 10 + 4i - 25i - 10i2 = 10 + 4(-1) - 25(-1) - 10(1) = 10 - 4 + 25 - 10 = 21 Complete the explanation and correct the error. Hint: The student incorre
While attempting to multiply the expression (2 - 5i)(5 + 2i), a student made a mistake. (2 - 5i)(5 + 2i) = 10 + 4i - 25i - 10i2 = 10 + 4(-1) - 25(-1) - 10(1) = 10 - 4 + 25 - 10 = 21 Complete the explanation and correct the error. Hint: The student incorre
