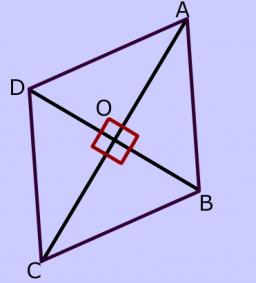
Diagonals in diamond
In the rhombus is given a = 160 cm, alpha = 60 degrees. Calculate the length of the diagonals.
Correct answer:
Tips for related online calculators
The Pythagorean theorem is the base for the right triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
- arithmetic
- square root
- planimetrics
- Pythagorean theorem
- polygon
- triangle
- rhombus
- diagonal
- The Law of Cosines
- goniometry and trigonometry
- cosine
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Rhombus 36
 Rhombus ABCD with side 8 cm long has diagonal BD 11.3 cm long. Find angle DAB.
Rhombus ABCD with side 8 cm long has diagonal BD 11.3 cm long. Find angle DAB. - Isosceles 83157
 Using the cosine theorem, prove that in an isosceles triangle ABC with base AB, c=2a cos α.
Using the cosine theorem, prove that in an isosceles triangle ABC with base AB, c=2a cos α. - Sides ratio and angles
 In triangle ABC, you know the ratio of side lengths a:b:c=3:4:6. Calculate the angle sizes of triangle ABC.
In triangle ABC, you know the ratio of side lengths a:b:c=3:4:6. Calculate the angle sizes of triangle ABC. - Using 4
 Using the law of cosines, find the measurement of leg b if the givens are B=20°, a=10, and c=15.
Using the law of cosines, find the measurement of leg b if the givens are B=20°, a=10, and c=15. - Three 235
 Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 80 degrees. Draw a picture and find the distance between A and B.
Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 80 degrees. Draw a picture and find the distance between A and B. - Piece of a wire
 A piece of wire is bent into the shape of a triangle. Two sides have lengths of 24 inches and 21 inches. The angle between these two sides is 55°. What is the length of the third side to the nearest hundredth of an inch? A: The length of the third side is
A piece of wire is bent into the shape of a triangle. Two sides have lengths of 24 inches and 21 inches. The angle between these two sides is 55°. What is the length of the third side to the nearest hundredth of an inch? A: The length of the third side is - A triangle 7
 A triangle lot has the dimensions a=15m, b=10m, and c=20m. What is the measure of the angle between the sides of b and c?
A triangle lot has the dimensions a=15m, b=10m, and c=20m. What is the measure of the angle between the sides of b and c? - Solve 13
 Solve the missing dimensions for the following triangle: Triangle ABC: AngleA=43 degrees, b=7.0cm, c=6.0cm Question 1. Angle B with units written as degrees Question 2. Angle C with units written as degrees Question 3. a, rounded to the nearest tenth of a
Solve the missing dimensions for the following triangle: Triangle ABC: AngleA=43 degrees, b=7.0cm, c=6.0cm Question 1. Angle B with units written as degrees Question 2. Angle C with units written as degrees Question 3. a, rounded to the nearest tenth of a - SAS calculation
 Given the triangle ABC, if side b is 31 ft., side c is 22 ft., and angle A is 47°, find side a. Please round to one decimal.
Given the triangle ABC, if side b is 31 ft., side c is 22 ft., and angle A is 47°, find side a. Please round to one decimal. - Triangle 75
 Triangle ABC has angle C bisected and intersected AB at D. Angle A measures 20 degrees, and angle B measures 40 degrees. The question is to determine AB-AC if length AD=1.
Triangle ABC has angle C bisected and intersected AB at D. Angle A measures 20 degrees, and angle B measures 40 degrees. The question is to determine AB-AC if length AD=1. - Loonie
 Loonie has three wooden sticks measuring 17 inches, 21 inches, and 25 inches. He lays them down to form a triangle. Find the measure of the angle enclosed by 17 inches and 21 inches. (Express answers to the nearest hundredths) (using the law of cosines)
Loonie has three wooden sticks measuring 17 inches, 21 inches, and 25 inches. He lays them down to form a triangle. Find the measure of the angle enclosed by 17 inches and 21 inches. (Express answers to the nearest hundredths) (using the law of cosines) - Binibini
 Binibini owns a triangular residential lot bounded by two roads intersecting at 70°. The sides of the lot along the road are 62m and 43m, respectively. Find the length of the fence needed to enclose the lot. (express answers to the nearest hundredths)
Binibini owns a triangular residential lot bounded by two roads intersecting at 70°. The sides of the lot along the road are 62m and 43m, respectively. Find the length of the fence needed to enclose the lot. (express answers to the nearest hundredths) - Designated 71874
 The patrol had started at a designated marching angle (an azimuth) of 13°. After 9 km, the azimuth's angle changed to 62°. The patrol went 10 km in this direction. Find the distance from where the patrol started.
The patrol had started at a designated marching angle (an azimuth) of 13°. After 9 km, the azimuth's angle changed to 62°. The patrol went 10 km in this direction. Find the distance from where the patrol started. - Big tower
 From the tower, which is 15 m high and 30 m from the river, the river's width appeared at an angle of 15°. How wide is the river in this place?
From the tower, which is 15 m high and 30 m from the river, the river's width appeared at an angle of 15°. How wide is the river in this place? - Magnitudes 64704
 The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '.
The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '. - Cosine
 Cosine and sine theorem: Calculate all missing values from triangle ABC. c = 2.9 cm; β = 28°; γ = 14° α =? °; a =? cm; b =? cm
Cosine and sine theorem: Calculate all missing values from triangle ABC. c = 2.9 cm; β = 28°; γ = 14° α =? °; a =? cm; b =? cm - Cosine
 Cosine and sine theorem: Calculate all missing values (sides and angles) of the triangle ABC. a = 20 cm; b = 15 cm; γ = 90°; c =? cm; α =? °; β =? °
Cosine and sine theorem: Calculate all missing values (sides and angles) of the triangle ABC. a = 20 cm; b = 15 cm; γ = 90°; c =? cm; α =? °; β =? °
