Slow saving in banks
How long will it take to save € 9,000 by depositing € 200 at the beginning of each year at 2% interest?
Correct answer:

Tips for related online calculators
Our percentage calculator will help you quickly calculate various typical tasks with percentages.
Do you want to convert time units like minutes to seconds?
Do you want to convert time units like minutes to seconds?
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Themes, topics:
Grade of the word problem:
Related math problems and questions:
- Sequences AP + GP
 The three numbers that make up the arithmetic sequence have the sum of 30. If we subtract from the first 5, the second 4, and keep the third, we get the geometric series. Find AP and GP members.
The three numbers that make up the arithmetic sequence have the sum of 30. If we subtract from the first 5, the second 4, and keep the third, we get the geometric series. Find AP and GP members. - Coloured numbers
 Mussel wrote four different natural numbers with colored markers: red, blue, green, and yellow. When the red number divides by blue, it gets the green number as an incomplete proportion, and yellow represents the remainder after this division. When it div
Mussel wrote four different natural numbers with colored markers: red, blue, green, and yellow. When the red number divides by blue, it gets the green number as an incomplete proportion, and yellow represents the remainder after this division. When it div - The Hotel
 The Holiday Hotel has the same number of rooms on each floor. Rooms are numbered with natural numerals sequentially from the first floor, no number is omitted, and each room has a different number. Three tourists arrived at the hotel. The first one was in
The Holiday Hotel has the same number of rooms on each floor. Rooms are numbered with natural numerals sequentially from the first floor, no number is omitted, and each room has a different number. Three tourists arrived at the hotel. The first one was in - GP sequence
 Find the remaining unknown characteristics in the finite geometric sequence, if given: a1 = 5, an = 320, sn = 635, n =? q =?
Find the remaining unknown characteristics in the finite geometric sequence, if given: a1 = 5, an = 320, sn = 635, n =? q =? - Finite geometric sequence
 Find the remaining unknown characteristics in the finite geometric sequence, if given: a1 = 18, an = 13122, sn = 19674, n =? q =?
Find the remaining unknown characteristics in the finite geometric sequence, if given: a1 = 18, an = 13122, sn = 19674, n =? q =? - Members
 A geometric sequence with six members has the sum of all six members equal to 63; the sum of the even members (that has an even index) has a value of 42. Find these members.
A geometric sequence with six members has the sum of all six members equal to 63; the sum of the even members (that has an even index) has a value of 42. Find these members. - The cylinder
 In a rotating cylinder, it is given: the surface of the shell (without bases) S = 96 cm² and the volume V = 192 cm cubic. Calculate the radius and height of this cylinder.
In a rotating cylinder, it is given: the surface of the shell (without bases) S = 96 cm² and the volume V = 192 cm cubic. Calculate the radius and height of this cylinder. - Rotary cylinder
 In the rotary cylinder it is given: surface S = 96 cm² and volume V = 192 cm cubic. Calculate its radius and height.
In the rotary cylinder it is given: surface S = 96 cm² and volume V = 192 cm cubic. Calculate its radius and height. - Faces diagonals
 If a cuboid's diagonals are x, y, and z (wall diagonals or three faces), find the cuboid volume. Solve for x=1.3, y=1, z=1.2
If a cuboid's diagonals are x, y, and z (wall diagonals or three faces), find the cuboid volume. Solve for x=1.3, y=1, z=1.2 - Two chords
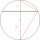 Calculate the length of chord AB and perpendicular chord BC to the circle if AB is 4 cm from the circle's center and BC 8 cm from the center.
Calculate the length of chord AB and perpendicular chord BC to the circle if AB is 4 cm from the circle's center and BC 8 cm from the center. - Sufficient 9391
 In Kocourkov, they use coins with only two values expressed in Kocourkov crowns by positive integers. With a sufficient number of such coins, it is possible to pay any integer amount greater than 53 cats’ crowns accurately and without return. However, we
In Kocourkov, they use coins with only two values expressed in Kocourkov crowns by positive integers. With a sufficient number of such coins, it is possible to pay any integer amount greater than 53 cats’ crowns accurately and without return. However, we - Geometric progressiob
 If the sum of four consecutive terms of a geometric progression is 80 and the arithmetic mean of the second and fourth terms is 30, then find terms.
If the sum of four consecutive terms of a geometric progression is 80 and the arithmetic mean of the second and fourth terms is 30, then find terms. - GP - three members
 The second and third of a geometric progression are 24 and 12(c+1), respectively, given that the sum of the first three terms of progression is 76. determine the value of c.
The second and third of a geometric progression are 24 and 12(c+1), respectively, given that the sum of the first three terms of progression is 76. determine the value of c. - Hyperbola equation
 Find the hyperbola equation with the center of S [0; 0], passing through the points: A [5; 3] B [8; -10]
Find the hyperbola equation with the center of S [0; 0], passing through the points: A [5; 3] B [8; -10] - Rectangular triangle
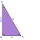 The lengths of the rectangular triangle sides with a longer leg of 12 cm form an arithmetic sequence. What is the area of the triangle?
The lengths of the rectangular triangle sides with a longer leg of 12 cm form an arithmetic sequence. What is the area of the triangle? - MO Z8-I-1 2018
 Fero and David meet daily in the elevator. One morning, they found that if they multiply their current age, they get 238. If they did the same after four years, this product would be 378. Determine the sum of the current ages of Fero and David.
Fero and David meet daily in the elevator. One morning, they found that if they multiply their current age, they get 238. If they did the same after four years, this product would be 378. Determine the sum of the current ages of Fero and David. - Right triangle eq2
 Find the lengths of the sides and the angles in the right triangle. Given area S = 210 and perimeter o = 70.
Find the lengths of the sides and the angles in the right triangle. Given area S = 210 and perimeter o = 70.
