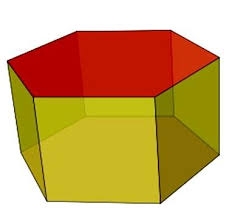
Regular hexagonal prism
Calculate the volume of a regular hexagonal prism whose body diagonals are 24cm and 25cm long.
Correct answer:
Tips for related online calculators
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- equation
- expression of a variable from the formula
- solid geometry
- space diagonal
- planimetrics
- Pythagorean theorem
- right triangle
- polygon
- area of a shape
- triangle
- diagonal
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Quadrilateral 70294
 The edge lengths of a quadrilateral prism are in the ratio a: b: c = 2:4:5. The surface of the prism is 57 cm². Calculate the volume.
The edge lengths of a quadrilateral prism are in the ratio a: b: c = 2:4:5. The surface of the prism is 57 cm². Calculate the volume. - Right-angled trapezoid
 A right-angled trapezoid with the measure of the acute angle of 50° is given. The lengths of its bases are 4 and 6 units. The volume of the solid obtained by rotation of the given trapezoid about the longer base is:
A right-angled trapezoid with the measure of the acute angle of 50° is given. The lengths of its bases are 4 and 6 units. The volume of the solid obtained by rotation of the given trapezoid about the longer base is: - Side wall planes
 Find the volume and surface of a cuboid whose side c is 30 cm long and the body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls.
Find the volume and surface of a cuboid whose side c is 30 cm long and the body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls. - Sphere submerged in the cone
 A right circular cone with a top width of 24 cm and an altitude of 8 cm is filled with water. A spherical steel ball with a radius of 3.0cm is submerged in the cone. Find the volume of water below the sphere.
A right circular cone with a top width of 24 cm and an altitude of 8 cm is filled with water. A spherical steel ball with a radius of 3.0cm is submerged in the cone. Find the volume of water below the sphere.
- Slant height 2
 A regular triangular pyramid with a slant height of 9 m has a volume of 50 m³. Find the lateral area of the pyramid.
A regular triangular pyramid with a slant height of 9 m has a volume of 50 m³. Find the lateral area of the pyramid. - Radiators
 Calculate the radiator output if it has a thermal gradient (difference between inlet water and return temperatures) a) 5°C b) 10°C c) 15°C d) 20°C A heating water volume flow is 45 kg/h. How fast the water flows from the supply pipe to the radiator e) DN1
Calculate the radiator output if it has a thermal gradient (difference between inlet water and return temperatures) a) 5°C b) 10°C c) 15°C d) 20°C A heating water volume flow is 45 kg/h. How fast the water flows from the supply pipe to the radiator e) DN1 - Richard
 Richard is conducting an experiment. Every time he flips a fair two-sided coin, he also rolls a six-sided die. What is the probability that the coin will land on tails and the die will land on an even number?
Richard is conducting an experiment. Every time he flips a fair two-sided coin, he also rolls a six-sided die. What is the probability that the coin will land on tails and the die will land on an even number? - Locker combination
 Todd forgot the first two numbers of his locker combination. The numbers can be any number 1 through 6. What is the probability that he will guess the first number correctly and the second number incorrectly?
Todd forgot the first two numbers of his locker combination. The numbers can be any number 1 through 6. What is the probability that he will guess the first number correctly and the second number incorrectly? - Multimodal or unimodal
 The weights (in kg) of 13 students of a class are 37,39,33,32,41,33,37,45,43,39, 33,40,39 Find the mode & media of this data (F) Is there more than one mode?
The weights (in kg) of 13 students of a class are 37,39,33,32,41,33,37,45,43,39, 33,40,39 Find the mode & media of this data (F) Is there more than one mode?
- Rhombus 36
 Rhombus ABCD with side 8 cm long has diagonal BD 11.3 cm long. Find angle DAB.
Rhombus ABCD with side 8 cm long has diagonal BD 11.3 cm long. Find angle DAB. - Third tests
 Third periodical tests are 98, 97, 86, 94, 90, 97, 91, and 94. Find the median of her grades and interpret the result.
Third periodical tests are 98, 97, 86, 94, 90, 97, 91, and 94. Find the median of her grades and interpret the result. - The median 2
 Here is a list of numbers: 9.9, 5.9, 3.6, 6.2, 8.9, 0.7, 4.4, 6.7, 9.9, 0.7 State the median. Give your answer as a decimal.
Here is a list of numbers: 9.9, 5.9, 3.6, 6.2, 8.9, 0.7, 4.4, 6.7, 9.9, 0.7 State the median. Give your answer as a decimal. - A population
 A population of fish starts at 8,000 and decreases by 6% per year. Use an exponential function to find the population of fish in 10 years.
A population of fish starts at 8,000 and decreases by 6% per year. Use an exponential function to find the population of fish in 10 years. - The mean 2
 The mean cost of 4 items was $39.96. The first item cost $28.50, the second item cost $41.25, and the third item cost $50. Find the cost of the fourth item.
The mean cost of 4 items was $39.96. The first item cost $28.50, the second item cost $41.25, and the third item cost $50. Find the cost of the fourth item.
- Correct mean and CV
 For a group of 100 students, the mean and coefficient of variation of their marks were found to be 60 and 25, respectively. Later, it was found that the scores 45 and 70 were wrongly entered as 40 and 27. Find the corrected mean and coefficient of variati
For a group of 100 students, the mean and coefficient of variation of their marks were found to be 60 and 25, respectively. Later, it was found that the scores 45 and 70 were wrongly entered as 40 and 27. Find the corrected mean and coefficient of variati - The capacitor
 The parallel square plates of a 4.5µF Teflon capacitor are 3.2 mm apart. What is the area of the plate?
The parallel square plates of a 4.5µF Teflon capacitor are 3.2 mm apart. What is the area of the plate? - IQ scores
 IQ scores are normally distributed with a mean of 100 and a standard deviation of 15. What percentage of the population scores higher than 125 on an IQ test?
IQ scores are normally distributed with a mean of 100 and a standard deviation of 15. What percentage of the population scores higher than 125 on an IQ test?
