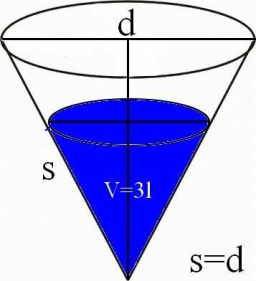
The funnel
The funnel has the shape of an equilateral cone. Calculate the area wetted with water if you pour 3 liters of water into the funnel.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- arithmetic
- cube root
- solid geometry
- cone
- surface area
- planimetrics
- area of a shape
- triangle
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Funnel
 The funnel has the shape of an equilateral cone. Calculate the surface wetted with water if we poured into the funnel 7.1 liters of water.
The funnel has the shape of an equilateral cone. Calculate the surface wetted with water if we poured into the funnel 7.1 liters of water. - Calculate 16513
 The conical funnel has a volume of 0.5 liters and a height of 7 cm. Calculate the radius of its upper edge.
The conical funnel has a volume of 0.5 liters and a height of 7 cm. Calculate the radius of its upper edge. - Water in aquarium
 The aquarium cuboid shape with a length of 25 cm and a width of 30 cm is 9 liters of water. Calculate the areas which are wetted with water.
The aquarium cuboid shape with a length of 25 cm and a width of 30 cm is 9 liters of water. Calculate the areas which are wetted with water. - Equilateral cone
 We pour so much water into a container with the shape of an equilateral cone, the base of which has a radius r = 6 cm, that one-third of the volume of the cone is filled. How high will the water reach if we turn the cone upside down?
We pour so much water into a container with the shape of an equilateral cone, the base of which has a radius r = 6 cm, that one-third of the volume of the cone is filled. How high will the water reach if we turn the cone upside down? - Container
 The container has a cylindrical shape, the base diameter is 0.8 m, and the area of the base is equal to the area of the wall. How many liters of water can we pour into the container?
The container has a cylindrical shape, the base diameter is 0.8 m, and the area of the base is equal to the area of the wall. How many liters of water can we pour into the container? - Fountain
 The stone fountain, which has the shape of a cylinder with a diameter of 3 m, is 70 cm deep. How many m² of stone is wetted with water?
The stone fountain, which has the shape of a cylinder with a diameter of 3 m, is 70 cm deep. How many m² of stone is wetted with water? - Cube-shaped 81023
 The cube-shaped pool is 50 m long and 16 m wide. They poured 12,000 hl of water into it. Calculate the surface area of the pool that is wetted by water.
The cube-shaped pool is 50 m long and 16 m wide. They poured 12,000 hl of water into it. Calculate the surface area of the pool that is wetted by water. - Aquarium
 There are 15 liters of water in a block-shaped aquarium with internal dimensions of the bottom of 25 cm and 30 cm. Find the area of water-wetted surfaces. Express the result in dm square.
There are 15 liters of water in a block-shaped aquarium with internal dimensions of the bottom of 25 cm and 30 cm. Find the area of water-wetted surfaces. Express the result in dm square. - The bottle
 The bottle contains 1.5 liters of mineral water. Pour all the water from the bottle into empty cups with a volume of 1/3 l. We will fill all but one to the brim. What part of the volume of the last cup is filled with water?
The bottle contains 1.5 liters of mineral water. Pour all the water from the bottle into empty cups with a volume of 1/3 l. We will fill all but one to the brim. What part of the volume of the last cup is filled with water? - Fire tank
 1428 hl of water is filled in a block-shaped fire tank with the edges of the base 12 m and 7 m. Calculate the area of water-wetted areas.
1428 hl of water is filled in a block-shaped fire tank with the edges of the base 12 m and 7 m. Calculate the area of water-wetted areas. - Water tank
 A 288 hectoliter of water was poured into the tank with dimensions of 12 m and 6 m bottom, and 2 m depth. What part of the volume of the tank water is occupied? Calculate the surface of the tank wetted with water.
A 288 hectoliter of water was poured into the tank with dimensions of 12 m and 6 m bottom, and 2 m depth. What part of the volume of the tank water is occupied? Calculate the surface of the tank wetted with water. - Water-wetted 35193
 The block-shaped pool with dimensions of 25 m and 12.5 m and a depth of 2 m is filled with 4/5 of water. Calculate the area of water-wetted areas.
The block-shaped pool with dimensions of 25 m and 12.5 m and a depth of 2 m is filled with 4/5 of water. Calculate the area of water-wetted areas. - Equilateral 80573
 The field has the shape of an equilateral triangle. Calculate its content if you know that the side is 280 meters long.
The field has the shape of an equilateral triangle. Calculate its content if you know that the side is 280 meters long. - Container 15093
 A cone-shaped container with a bottom diameter of 60 cm and a side length of 0.5 m is filled with water. We pour the water into a container with the face of a cylinder with a radius of 3dm and a height of 20cm. Will the cylinder overflow or not be complet
A cone-shaped container with a bottom diameter of 60 cm and a side length of 0.5 m is filled with water. We pour the water into a container with the face of a cylinder with a radius of 3dm and a height of 20cm. Will the cylinder overflow or not be complet - Octagonal prism vase
 We can pour 0.7 l of water into an octagonal prism vase. The vase has the bottom has an area of 25 cm square and a thickness of 12 mm. What is the height of the vase?
We can pour 0.7 l of water into an octagonal prism vase. The vase has the bottom has an area of 25 cm square and a thickness of 12 mm. What is the height of the vase? - Axial section
 The axial section of the cone is an equilateral triangle with an area 208 m². Calculate the volume of the cone.
The axial section of the cone is an equilateral triangle with an area 208 m². Calculate the volume of the cone. - Cylindrical 19773
 When we pour 3 l of water into a cylindrical tin can, the water rises to 20 cm. Calculate the average can.
When we pour 3 l of water into a cylindrical tin can, the water rises to 20 cm. Calculate the average can.
