Quadrilateral pyramid
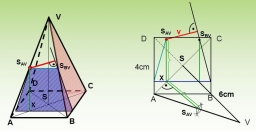
The height of a regular quadrilateral pyramid is 6.5 cm, and the angle between the base and the side wall is 42°. Calculate the surface area and volume of the body—round calculations to 1 decimal place.
Correct answer:
Tips for related online calculators
Need help calculating sum, simplifying, or multiplying fractions? Try our fraction calculator.
See also our right triangle calculator.
Do you know the volume and unit volume, and want to convert volume units?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
See also our right triangle calculator.
Do you know the volume and unit volume, and want to convert volume units?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- arithmetic
- square root
- solid geometry
- pyramid
- surface area
- planimetrics
- Pythagorean theorem
- right triangle
- area of a shape
- triangle
- square
- diagonal
- quadrilateral
- numbers
- fractions
- goniometry and trigonometry
- tangent
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Create 6
 Create a new drink can that will double the volume of the original can used. Dimensions of the can: 6cm diameter and 10cm height. You are to double the volume with the least amount of additional aluminum needed for the new can. There are 3 options : Optio
Create a new drink can that will double the volume of the original can used. Dimensions of the can: 6cm diameter and 10cm height. You are to double the volume with the least amount of additional aluminum needed for the new can. There are 3 options : Optio - Quadrilateral 70294
 The edge lengths of a quadrilateral prism are in the ratio a: b: c = 2:4:5. The surface of the prism is 57 cm². Calculate the volume.
The edge lengths of a quadrilateral prism are in the ratio a: b: c = 2:4:5. The surface of the prism is 57 cm². Calculate the volume. - Prism - right isosceles
 Find the volume and surface of a prism with a height of 120 mm, the base of which is a right isosceles triangle with a leg length of 5 cm.
Find the volume and surface of a prism with a height of 120 mm, the base of which is a right isosceles triangle with a leg length of 5 cm. - Side wall planes
 Find the volume and surface of a cuboid whose side c is 30 cm long and the body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls.
Find the volume and surface of a cuboid whose side c is 30 cm long and the body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls. - Slant height 2
 A regular triangular pyramid with a slant height of 9 m has a volume of 50 m³. Find the lateral area of the pyramid.
A regular triangular pyramid with a slant height of 9 m has a volume of 50 m³. Find the lateral area of the pyramid. - Cylinder S,V
 What is the volume and surface area of a cylinder whose base has a diameter of 3.15 cm and a height of 25 cm?
What is the volume and surface area of a cylinder whose base has a diameter of 3.15 cm and a height of 25 cm? - Quadrilateral 58663
 They melted the steel part in the shape of a truncated quadrilateral needle and produced three identical cubes. Determine the surface area of one cube if the edges of the bases of the pyramid are 30 mm and 80 mm and the pyramid's height is 60 mm. I don't
They melted the steel part in the shape of a truncated quadrilateral needle and produced three identical cubes. Determine the surface area of one cube if the edges of the bases of the pyramid are 30 mm and 80 mm and the pyramid's height is 60 mm. I don't - Right-angled triangle base
 Find the volume and surface area of a triangular prism with a right-angled triangle base if the length of the prism base legs are 7.2 cm and 4.7 cm and the height of a prism is 24 cm.
Find the volume and surface area of a triangular prism with a right-angled triangle base if the length of the prism base legs are 7.2 cm and 4.7 cm and the height of a prism is 24 cm. - Triangular 46641
 The regular triangular pyramid ABCDV has a base edge length of 8 cm and a height of 7 cm. Calculate the pyramid's surface area and volume.
The regular triangular pyramid ABCDV has a base edge length of 8 cm and a height of 7 cm. Calculate the pyramid's surface area and volume. - Cube-shaped box
 The cube-shaped box is filled to the brim with 2 liters of milk. Calculate the edge and surface of the box.
The cube-shaped box is filled to the brim with 2 liters of milk. Calculate the edge and surface of the box. - Geometric Solid
 A concrete pipe is 1.0 m long. Its inside and outside diameters are 60 cm and 75 cm, respectively. What is the volume of the concrete (cubic meters) needed to make 25 pcs of pipe?
A concrete pipe is 1.0 m long. Its inside and outside diameters are 60 cm and 75 cm, respectively. What is the volume of the concrete (cubic meters) needed to make 25 pcs of pipe? - A frustum
 A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume.
A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume. - Tent - spherical cap
 I have a tent in the shape of a spherical cap. Assume we want the volume to be 4 cubic meters, to sleep two or three people. Assume that the material making up the dome of the ten is twice as expensive per square as the material touching the ground. What
I have a tent in the shape of a spherical cap. Assume we want the volume to be 4 cubic meters, to sleep two or three people. Assume that the material making up the dome of the ten is twice as expensive per square as the material touching the ground. What - Januka
 Januka and her father were going to the tent. They found that their old tent was torn. Their mother suggested that they sew a tent whose walls would be made of 4 identical isosceles triangles. Their lower side is 2 m long, and the height is also 2 m. Then
Januka and her father were going to the tent. They found that their old tent was torn. Their mother suggested that they sew a tent whose walls would be made of 4 identical isosceles triangles. Their lower side is 2 m long, and the height is also 2 m. Then - A lamp
 A lamp shade like that of a frustum has a height of 12 cm and an upper and lower diameter of 10 cm and 20 cm. What area of materials is required to cover the curved surface of the frustum?
A lamp shade like that of a frustum has a height of 12 cm and an upper and lower diameter of 10 cm and 20 cm. What area of materials is required to cover the curved surface of the frustum? - Saria
 Saria is wrapping a gift for her mother. The gift box is in the shape of a rectangular prism and is 5 centimeters high, 25 centimeters long, and 40 centimeters wide. How much wrapping paper will you need to wrap the gift box?
Saria is wrapping a gift for her mother. The gift box is in the shape of a rectangular prism and is 5 centimeters high, 25 centimeters long, and 40 centimeters wide. How much wrapping paper will you need to wrap the gift box? - Cross-section 81879
 The castle has a length of 4 m and a cross-section in the shape of a square whose side is 15 cm long. Eight such castles must be painted. One kilogram can is enough for 6 m² of coating. How many cans of paint should be bought?
The castle has a length of 4 m and a cross-section in the shape of a square whose side is 15 cm long. Eight such castles must be painted. One kilogram can is enough for 6 m² of coating. How many cans of paint should be bought?
