Trigonometric functions
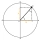
In the right triangle is:
tg α=24
Find the value of s and k:
sin α=20s
cos α=20k
tg α=24
Find the value of s and k:
sin α=20s
cos α=20k
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
- arithmetic
- square root
- planimetrics
- Pythagorean theorem
- right triangle
- triangle
- numbers
- real numbers
- goniometry and trigonometry
- sine
- cosine
- tangent
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- X-triangle
 Find the length of the x segment in the given triangle drawings.
Find the length of the x segment in the given triangle drawings. - Trigonometric fx
 When an acute angle φ is in the standard position, its terminal side passes through point P (1,3). Find trigonometric functions of angle θ : sin φ, cos φ, tan φ, cotan φ.
When an acute angle φ is in the standard position, its terminal side passes through point P (1,3). Find trigonometric functions of angle θ : sin φ, cos φ, tan φ, cotan φ. - Three 235
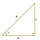
 Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 80 degrees. Draw a picture and find the distance between A and B.
Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 80 degrees. Draw a picture and find the distance between A and B. - A right
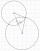
 A right triangle has side lengths a=3, b=5, and c=4, as shown below. Use these lengths to find tan x, sin x, and cos x.
A right triangle has side lengths a=3, b=5, and c=4, as shown below. Use these lengths to find tan x, sin x, and cos x. - Subtract polar forms
 Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form
Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form - Conjugate coordinates
 If the rectangular conjugate of the polar vector 12 angle 35 degrees is equal to x+yi, find the sum of x and y.
If the rectangular conjugate of the polar vector 12 angle 35 degrees is equal to x+yi, find the sum of x and y. - Let z 2
 Let z = 2 - sqrt(3i). Find z6 and express your answer in rectangular form. if z = 2 - 2sqrt(3 i) then r = |z| = sqrt(2 ^ 2 + (- 2sqrt(3)) ^ 2) = sqrt(16) = 4 and theta = tan -2√3/2=-π/3
Let z = 2 - sqrt(3i). Find z6 and express your answer in rectangular form. if z = 2 - 2sqrt(3 i) then r = |z| = sqrt(2 ^ 2 + (- 2sqrt(3)) ^ 2) = sqrt(16) = 4 and theta = tan -2√3/2=-π/3 - In the desert
 A man wondering in the desert walks 5.7 miles in the direction S 26° W. He then turns 90° and walks 9 miles in the direction N 49° W. At that time, how far is he from his starting point, and what is his bearing from his starting point?
A man wondering in the desert walks 5.7 miles in the direction S 26° W. He then turns 90° and walks 9 miles in the direction N 49° W. At that time, how far is he from his starting point, and what is his bearing from his starting point? - Felix
 Calculate how much land Felix Baumgartner saw after jumping from 36 km above the ground. The radius of the Earth is R = 6378 km.
Calculate how much land Felix Baumgartner saw after jumping from 36 km above the ground. The radius of the Earth is R = 6378 km. - Crosswind
 A plane is traveling 45 degrees N of E at 320 km/h when it comes across a current from S of E at 115 degrees of 20 km/h. What are the airplane's new course and speed?
A plane is traveling 45 degrees N of E at 320 km/h when it comes across a current from S of E at 115 degrees of 20 km/h. What are the airplane's new course and speed? - Acceleration 79164
 A skier goes down a slope 66 m long in a uniformly accelerated motion in 10 seconds. With what acceleration was it moving, and what is the slope of the slope?
A skier goes down a slope 66 m long in a uniformly accelerated motion in 10 seconds. With what acceleration was it moving, and what is the slope of the slope? - Solve 13
 Solve the missing dimensions for the following triangle: Triangle ABC: AngleA=43 degrees, b=7.0cm, c=6.0cm Question 1. Angle B with units written as degrees Question 2. Angle C with units written as degrees Question 3. a, rounded to the nearest tenth of a
Solve the missing dimensions for the following triangle: Triangle ABC: AngleA=43 degrees, b=7.0cm, c=6.0cm Question 1. Angle B with units written as degrees Question 2. Angle C with units written as degrees Question 3. a, rounded to the nearest tenth of a - Sin cos tan
 If cos y = 0.8, 0° ≤ y ≤ 90°, find the value of (4 tan y) / (cos y-sin y)
If cos y = 0.8, 0° ≤ y ≤ 90°, find the value of (4 tan y) / (cos y-sin y) - A ship
 A ship has been spotted by two lighthouses, A and B, as shown in the figure. What is the distance from the ship to Lighthouse A to the nearest tenth? Figure - the distance between lighthouses A and B is 40 nautical miles. From A is seen in view angle 57°
A ship has been spotted by two lighthouses, A and B, as shown in the figure. What is the distance from the ship to Lighthouse A to the nearest tenth? Figure - the distance between lighthouses A and B is 40 nautical miles. From A is seen in view angle 57° - A Ferris wheel
 A Ferris wheel with a diameter of 100 feet makes five revolutions every 8 minutes. The base of the wheel is 4 feet above the ground. Your friend gets on at 3 PM sharp. a) Write an equation to express the height in feet of your friend at any given time in
A Ferris wheel with a diameter of 100 feet makes five revolutions every 8 minutes. The base of the wheel is 4 feet above the ground. Your friend gets on at 3 PM sharp. a) Write an equation to express the height in feet of your friend at any given time in - Triangle 75
 Triangle ABC has angle C bisected and intersected AB at D. Angle A measures 20 degrees, and angle B measures 40 degrees. The question is to determine AB-AC if length AD=1.
Triangle ABC has angle C bisected and intersected AB at D. Angle A measures 20 degrees, and angle B measures 40 degrees. The question is to determine AB-AC if length AD=1. - A flagpole
 A flagpole is leaning at an angle of 107° with the ground. A string fastened to the top of the flagpole is holding up the pole. The string makes an angle of 38° with the ground, and the flagpole is 8 m long. What is the length of the string?
A flagpole is leaning at an angle of 107° with the ground. A string fastened to the top of the flagpole is holding up the pole. The string makes an angle of 38° with the ground, and the flagpole is 8 m long. What is the length of the string?
