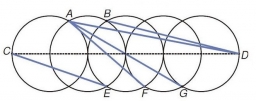
Five circles
On the line segment CD = 6 there are five circles with one radius at regular intervals. Find the lengths of the lines AD, AF, AG, BD, and CE.
Correct answer:
Tips for related online calculators
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- arithmetic
- square root
- planimetrics
- Pythagorean theorem
- right triangle
- circle
- triangle
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Intersection 7247
 On side AB of triangle ABC, points D and E are given such that |AD| = |DE| = |EB|. Points A and B are the midpoints of segments CF and CG. Line CD intersects line FB at point I, and line CE intersects line AG at point J. Prove that the intersection of lin
On side AB of triangle ABC, points D and E are given such that |AD| = |DE| = |EB|. Points A and B are the midpoints of segments CF and CG. Line CD intersects line FB at point I, and line CE intersects line AG at point J. Prove that the intersection of lin - There 35
 There are three points on a straight line: A, BC. If CD = 8x, DE = 3, and CE = x + 10, what is CD? Simplify your answer and write it as a proper fraction, mixed number, or integer.
There are three points on a straight line: A, BC. If CD = 8x, DE = 3, and CE = x + 10, what is CD? Simplify your answer and write it as a proper fraction, mixed number, or integer. - Diagonal in rectangle
 In the ABCD rectangle is the center of BC, point E, and point F is the center of the CD. Prove that the lines AE and AF divide diagonal BD into three equal parts.
In the ABCD rectangle is the center of BC, point E, and point F is the center of the CD. Prove that the lines AE and AF divide diagonal BD into three equal parts. - triangle 5420
 Two pairs of parallel lines, AB to CD and AC to BD, are given. Point E lies on the line BD, point F is the midpoint of the segment BD, point G is the midpoint of the segment CD, and the area of the triangle ACE is 20 cm². Determine the area of triangl
Two pairs of parallel lines, AB to CD and AC to BD, are given. Point E lies on the line BD, point F is the midpoint of the segment BD, point G is the midpoint of the segment CD, and the area of the triangle ACE is 20 cm². Determine the area of triangl - Construct 30121
 Point B is a vertex of rectangle ABCD. The diagonal BD of this rectangle lies on the line p. Point X is an interior point of side AD of rectangle ABCD, and point Y is an internal point of side CD. Construct the missing vertices D, A, and C of rectangle AB
Point B is a vertex of rectangle ABCD. The diagonal BD of this rectangle lies on the line p. Point X is an interior point of side AD of rectangle ABCD, and point Y is an internal point of side CD. Construct the missing vertices D, A, and C of rectangle AB - Trapezium ABCD
 The figure shows ABDC is a trapezium in which AB || CD. Line segments RN and LM are drawn parallel to AB such that AJ=JK=KP. If AB=0.5m and AP=BQ=1.8m, find the lengths of AC, BD, RN, and LM. angle D=angle C=60
The figure shows ABDC is a trapezium in which AB || CD. Line segments RN and LM are drawn parallel to AB such that AJ=JK=KP. If AB=0.5m and AP=BQ=1.8m, find the lengths of AC, BD, RN, and LM. angle D=angle C=60 - Angle of two lines
 There is a regular quadrangular pyramid ABCDV; | AB | = 4 cm; height v = 6 cm. Determine the angles of lines AD and BV.
There is a regular quadrangular pyramid ABCDV; | AB | = 4 cm; height v = 6 cm. Determine the angles of lines AD and BV. - MO - triangles
 On the AB and AC sides of the ABC triangle lies successive points E and F, and on segment EF lie point D. The EF and BC lines are parallel. It is true this ratio FD:DE = AE:EB = 2:1. The area of the ABC triangle is 27 hectares, and line segments EF, AD, a
On the AB and AC sides of the ABC triangle lies successive points E and F, and on segment EF lie point D. The EF and BC lines are parallel. It is true this ratio FD:DE = AE:EB = 2:1. The area of the ABC triangle is 27 hectares, and line segments EF, AD, a - Three lines
 At 6 AM, three bus lines depart from the station. The first line has an interval of 24 minutes. The second line has an interval of 15 minutes. The third line runs at regular intervals of more than 1 minute. The third line runs at the same time as the firs
At 6 AM, three bus lines depart from the station. The first line has an interval of 24 minutes. The second line has an interval of 15 minutes. The third line runs at regular intervals of more than 1 minute. The third line runs at the same time as the firs - Trapezoid ABCD
 ABDC is a trapezoid in which AB and CD are parallel sides measuring 6 and 9, respectively. Angles ABC and BCD are both right angles. Find the length of segment BD.
ABDC is a trapezoid in which AB and CD are parallel sides measuring 6 and 9, respectively. Angles ABC and BCD are both right angles. Find the length of segment BD. - Deviation of the lines
 Find the deviation of the lines AG BH in the ABCDEFGH box-cuboid if given | AB | = 3cm, | AD | = 2cm, | AE | = 4cm
Find the deviation of the lines AG BH in the ABCDEFGH box-cuboid if given | AB | = 3cm, | AD | = 2cm, | AE | = 4cm - Circles
 In the circle with a radius, 7.5 cm is constructed of two parallel chords whose lengths are 9 cm and 12 cm. Calculate the distance of these chords (if there are two possible solutions, write both).
In the circle with a radius, 7.5 cm is constructed of two parallel chords whose lengths are 9 cm and 12 cm. Calculate the distance of these chords (if there are two possible solutions, write both). - Intervals 3487
 The four teams left the terminal together at 5:00 in the morning. Line A runs at 15-minute intervals, line B at 6-minute intervals, line C at 20-minute intervals, and line D at 8-minute intervals. What time did all four lines leave the terminal together a
The four teams left the terminal together at 5:00 in the morning. Line A runs at 15-minute intervals, line B at 6-minute intervals, line C at 20-minute intervals, and line D at 8-minute intervals. What time did all four lines leave the terminal together a - Individual 6270
 Divide three lines with lengths of 12 cm, 24 cm, and 64 cm into equally long and, at the same time, the most extended possible parts. How long will the individual parts be, and how many will there be?
Divide three lines with lengths of 12 cm, 24 cm, and 64 cm into equally long and, at the same time, the most extended possible parts. How long will the individual parts be, and how many will there be? - Rhombus construction
 Construct ABCD rhombus if its diagonal AC=9 cm and side AB = 6 cm. Inscribe a circle in it, touching all sides.
Construct ABCD rhombus if its diagonal AC=9 cm and side AB = 6 cm. Inscribe a circle in it, touching all sides. - Quadrilateral 80729
 Quadrilateral ABCD has side lengths AB=13cm, CD=3cm, AD=4cm. Angles ACB and ADC are right angles. Calculate the perimeter of quadrilateral ABCD.
Quadrilateral ABCD has side lengths AB=13cm, CD=3cm, AD=4cm. Angles ACB and ADC are right angles. Calculate the perimeter of quadrilateral ABCD. - Suppose
 Suppose you know that the length of a line segment is 15, x2=6, y2=14, and x1= -3. Find the possible value of y1. Is there more than one possible answer? Why or why not?
Suppose you know that the length of a line segment is 15, x2=6, y2=14, and x1= -3. Find the possible value of y1. Is there more than one possible answer? Why or why not?
