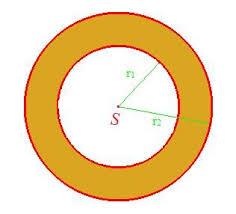
Circular ring
A square with an area of 16 centimeters is inscribed circle k1 and described to circle k2. Calculate the area of the circular ring, which circles k1, and k2 form.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Trim the bushes
 Mason is always helping him to trim the bushes. The area A had a length of 14 m and a breadth of 7 m, and if we are going to combine A and B, the equal is 215 m². The question is: what is the area of B?
Mason is always helping him to trim the bushes. The area A had a length of 14 m and a breadth of 7 m, and if we are going to combine A and B, the equal is 215 m². The question is: what is the area of B? - ET inscribed circle
 An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region.
An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region. - A farmer 9
 A farmer has 3 hectares of an orchard. ½ of the land is occupied by apples, ⅙ of the remainder is occupied by lemon trees, and tree tomatoes occupy the rest of it. Find the fraction of the land occupied by tree tomatoes.
A farmer has 3 hectares of an orchard. ½ of the land is occupied by apples, ⅙ of the remainder is occupied by lemon trees, and tree tomatoes occupy the rest of it. Find the fraction of the land occupied by tree tomatoes. - Linda
 Linda gave her sister 2/5 of her money, spent 1/3, and saved the remainder. If Linda saved $28.00, how much money did she have at first?
Linda gave her sister 2/5 of her money, spent 1/3, and saved the remainder. If Linda saved $28.00, how much money did she have at first?
- An electorate
 In an electorate, 3/4 th of the voters are Tamils. Of the remaining 2/3 rd are Muslims, and the others are Sinhalese. If the number of Sinhalese in that electorate is 587, find the number of voters in that electorate.
In an electorate, 3/4 th of the voters are Tamils. Of the remaining 2/3 rd are Muslims, and the others are Sinhalese. If the number of Sinhalese in that electorate is 587, find the number of voters in that electorate. - The radius 2
 The radius of a circle is increased by 5%. What is the percentage increase in their circumference area?
The radius of a circle is increased by 5%. What is the percentage increase in their circumference area? - Sonya
 Sonya, Jill, and Donna run each Monday. Jill ran 6/12 of an hour, and Donna ran 5/12 of an hour. If the girls ran a total of one whole hour, what fraction of an hour did Sonya run?
Sonya, Jill, and Donna run each Monday. Jill ran 6/12 of an hour, and Donna ran 5/12 of an hour. If the girls ran a total of one whole hour, what fraction of an hour did Sonya run? - Merly
 Merly prepared the table for lunch. She put a place mat that measures 5 dm long and 3 dm wide; she placed a plate on it with a diameter of 3 dm. How many mats can be seen on the table?
Merly prepared the table for lunch. She put a place mat that measures 5 dm long and 3 dm wide; she placed a plate on it with a diameter of 3 dm. How many mats can be seen on the table? - A goat 2
 As shown, a goat is tied at one corner of a rectangular shed by a 5-meter-long rope. The shed measures 3 m by 2 m and is surrounded by grassland. What is the area of the grassland in which the goat can graze? Give your answer to the nearest m².
As shown, a goat is tied at one corner of a rectangular shed by a 5-meter-long rope. The shed measures 3 m by 2 m and is surrounded by grassland. What is the area of the grassland in which the goat can graze? Give your answer to the nearest m².
- Perimeter 81600
 The radius of the circular bed is 2 m. Around it is an area filled with sand, the border of which is formed by the sides of a square with a length of 5 m and the bed's perimeter. Calculate the volume of the area covered with sand.
The radius of the circular bed is 2 m. Around it is an area filled with sand, the border of which is formed by the sides of a square with a length of 5 m and the bed's perimeter. Calculate the volume of the area covered with sand. - Tool room
 A 9' x 15' tool room was enlarged to 11' x 20'. How many square feet of floor space was added?
A 9' x 15' tool room was enlarged to 11' x 20'. How many square feet of floor space was added? - Jodi is
 Jodi is cutting out pieces of paper that measure 8 1/2 inches by 11 inches from a larger sheet of paper that has an area of 1,000 square inches. What is the area of each piece of paper that Jodi is cutting out?
Jodi is cutting out pieces of paper that measure 8 1/2 inches by 11 inches from a larger sheet of paper that has an area of 1,000 square inches. What is the area of each piece of paper that Jodi is cutting out? - ABC gifts
 Arthur had 30 dollars to spend on three gifts. He spent 9 3/4 dollars on gift A and 4 1/2 dollars on gift B. How much money did he have left for gift C?
Arthur had 30 dollars to spend on three gifts. He spent 9 3/4 dollars on gift A and 4 1/2 dollars on gift B. How much money did he have left for gift C? - The kitchen 2
 The kitchen, 5m by 3.5m, has a cupboard covering 2m by 0.75m of the floor. What area of the floor remains uncovered?
The kitchen, 5m by 3.5m, has a cupboard covering 2m by 0.75m of the floor. What area of the floor remains uncovered?
- Pearl
 Pearl wants to buy grass seed to cover her whole lawn with dimensions 7 x 11 meters, except for the pool. The pool is 5 3/4m by 3 1/2 m. Find the area the grass seed needs to cover.
Pearl wants to buy grass seed to cover her whole lawn with dimensions 7 x 11 meters, except for the pool. The pool is 5 3/4m by 3 1/2 m. Find the area the grass seed needs to cover. - A piece 5
 A piece of cloth is laid at the center of a table 80 cm long and 60 cm wide, and it leaves 5 cm all around. Find the area which is not covered by the piece of cloth.
A piece of cloth is laid at the center of a table 80 cm long and 60 cm wide, and it leaves 5 cm all around. Find the area which is not covered by the piece of cloth. - A square 3
 A square (with side b=2ft) is removed from the right-hand corner of a square board with side a= 12 ft. What is the area of the remaining board in square feet?
A square (with side b=2ft) is removed from the right-hand corner of a square board with side a= 12 ft. What is the area of the remaining board in square feet?
