Biquadratic
By introducing a new variable, solve the biquadratic equation:
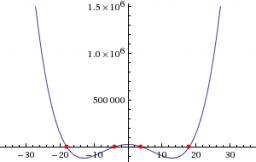
−x4+277x2−15876=0
−x4+277x2−15876=0
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Book Store
 The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w
The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w - Right triangle generator
 Detective Harry Thomson found on the Internet a generator of the lengths of the sides of right triangles according to which he must apply: a = 2xy, b = x² - y², c = x² + y², where are natural numbers and x & gt; y. Is it a working generator?
Detective Harry Thomson found on the Internet a generator of the lengths of the sides of right triangles according to which he must apply: a = 2xy, b = x² - y², c = x² + y², where are natural numbers and x & gt; y. Is it a working generator? - Members
 A geometric sequence with six members has the sum of all six members equal to 63; the sum of the even members (that has an even index) has a value of 42. Find these members.
A geometric sequence with six members has the sum of all six members equal to 63; the sum of the even members (that has an even index) has a value of 42. Find these members. - Given 2
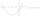 Given g(x)=x²+x+1 where x=t². What is g(t²)?
Given g(x)=x²+x+1 where x=t². What is g(t²)?
- Polynomial roots
 Find the other zeroes of the polynomial 2x4+3x³-3x²-6x-2, if two of them are root2 & -root2
Find the other zeroes of the polynomial 2x4+3x³-3x²-6x-2, if two of them are root2 & -root2 - Truncated pyramid
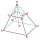 The truncated regular quadrilateral pyramid has a volume of 74 cm3, a height v = 6 cm, and an area of the lower base 15 cm² greater than the upper base's area. Calculate the area of the upper base.
The truncated regular quadrilateral pyramid has a volume of 74 cm3, a height v = 6 cm, and an area of the lower base 15 cm² greater than the upper base's area. Calculate the area of the upper base. - Sequences AP + GP
 The three numbers that make up the arithmetic sequence have the sum of 30. If we subtract from the first 5, the second 4, and keep the third, we get the geometric series. Find AP and GP members.
The three numbers that make up the arithmetic sequence have the sum of 30. If we subtract from the first 5, the second 4, and keep the third, we get the geometric series. Find AP and GP members. - The cylinder
 In a rotating cylinder, it is given: the surface of the shell (without bases) S = 96 cm² and the volume V = 192 cm cubic. Calculate the radius and height of this cylinder.
In a rotating cylinder, it is given: the surface of the shell (without bases) S = 96 cm² and the volume V = 192 cm cubic. Calculate the radius and height of this cylinder. - Rotary cylinder
 In the rotary cylinder it is given: surface S = 96 cm² and volume V = 192 cm cubic. Calculate its radius and height.
In the rotary cylinder it is given: surface S = 96 cm² and volume V = 192 cm cubic. Calculate its radius and height.
- Land boundary
 The land is a right triangle. Its hypotenuse is 30 meters long, and its circumference is 72 meters. What are the sizes of the remaining sides of the land boundary?
The land is a right triangle. Its hypotenuse is 30 meters long, and its circumference is 72 meters. What are the sizes of the remaining sides of the land boundary? - Faces diagonals
 If a cuboid's diagonals are x, y, and z (wall diagonals or three faces), find the cuboid volume. Solve for x=1.3, y=1, z=1.2
If a cuboid's diagonals are x, y, and z (wall diagonals or three faces), find the cuboid volume. Solve for x=1.3, y=1, z=1.2 - Two chords
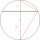 Calculate the length of chord AB and perpendicular chord BC to the circle if AB is 4 cm from the circle's center and BC 8 cm from the center.
Calculate the length of chord AB and perpendicular chord BC to the circle if AB is 4 cm from the circle's center and BC 8 cm from the center. - Geometric progressiob
 If the sum of four consecutive terms of a geometric progression is 80 and the arithmetic mean of the second and fourth terms is 30, then find terms.
If the sum of four consecutive terms of a geometric progression is 80 and the arithmetic mean of the second and fourth terms is 30, then find terms. - Three members GP
 The sum of three numbers in GP (geometric progression) is 21, and the sum of their squares is 189. Find the numbers.
The sum of three numbers in GP (geometric progression) is 21, and the sum of their squares is 189. Find the numbers.
- Eq2 2
 Solve the following equation with quadratic members and rational function: (x²+1)/(x-4) + (x²-1)/(x+3) = 23
Solve the following equation with quadratic members and rational function: (x²+1)/(x-4) + (x²-1)/(x+3) = 23 - Hyperbola equation
 Find the hyperbola equation with the center of S [0; 0], passing through the points: A [5; 3] B [8; -10]
Find the hyperbola equation with the center of S [0; 0], passing through the points: A [5; 3] B [8; -10] - Diamond diagonals
 Find the diamond diagonal's lengths if the area is 156 cm² and the side is 13 cm long.
Find the diamond diagonal's lengths if the area is 156 cm² and the side is 13 cm long.
