Pyramid in cube
In a cube with an edge 12 dm long, we have an inscribed pyramid with the apex at the center of the cube's upper wall. Calculate the volume and surface area of the pyramid.
Correct answer:
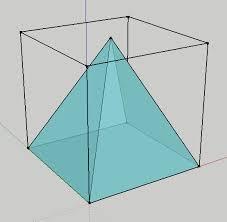
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- solid geometry
- cube
- pyramid
- surface area
- planimetrics
- Pythagorean theorem
- right triangle
- triangle
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- The height of prism
 A right triangle forms the base of the vertical prism with perpendiculars 30 cm and 40 cm long. This prism has the same volume as a cube with an edge length of 3 dm. Find its height in cm.
A right triangle forms the base of the vertical prism with perpendiculars 30 cm and 40 cm long. This prism has the same volume as a cube with an edge length of 3 dm. Find its height in cm. - Quadrilateral 58663
 They melted the steel part in the shape of a truncated quadrilateral needle and produced three identical cubes. Determine the surface area of one cube if the edges of the bases of the pyramid are 30 mm and 80 mm and the pyramid's height is 60 mm. I don't
They melted the steel part in the shape of a truncated quadrilateral needle and produced three identical cubes. Determine the surface area of one cube if the edges of the bases of the pyramid are 30 mm and 80 mm and the pyramid's height is 60 mm. I don't - Cube-shaped box
 The cube-shaped box is filled to the brim with 2 liters of milk. Calculate the edge and surface of the box.
The cube-shaped box is filled to the brim with 2 liters of milk. Calculate the edge and surface of the box. - Building blocks
 Rosa bought a set of building blocks for her younger brother, Owen, for his birthday. Owen opened the gift and immediately used all 35 blocks in the set to build a tower shaped like a rectangular prism. Each block is a cube that is 1 1/2 inches along each
Rosa bought a set of building blocks for her younger brother, Owen, for his birthday. Owen opened the gift and immediately used all 35 blocks in the set to build a tower shaped like a rectangular prism. Each block is a cube that is 1 1/2 inches along each
- Geometric Solid
 A concrete pipe is 1.0 m long. Its inside and outside diameters are 60 cm and 75 cm, respectively. What is the volume of the concrete (cubic meters) needed to make 25 pcs of pipe?
A concrete pipe is 1.0 m long. Its inside and outside diameters are 60 cm and 75 cm, respectively. What is the volume of the concrete (cubic meters) needed to make 25 pcs of pipe? - Perfect square or cube
 Would you classify 324 as a perfect square, perfect cube, both, or neither? ...
Would you classify 324 as a perfect square, perfect cube, both, or neither? ... - A cube 3
 A cube of edge 100 cm has the same volume as a cube of edge 1 m. how many cubic centimeters make 1 cubic meter?
A cube of edge 100 cm has the same volume as a cube of edge 1 m. how many cubic centimeters make 1 cubic meter? - A cube 2
 A cube has an edge length of 4 cm. Then its volume is:
A cube has an edge length of 4 cm. Then its volume is: - Beezlebum's
 Beezlebum's Toy Store can't keep its stackable block set in stock! The blocks completely fill a box shaped like a rectangular prism that is 14 inches long, 14 inches wide, and 21 inches tall. The cube-shaped blocks in the set are 3.5 inches along each edg
Beezlebum's Toy Store can't keep its stackable block set in stock! The blocks completely fill a box shaped like a rectangular prism that is 14 inches long, 14 inches wide, and 21 inches tall. The cube-shaped blocks in the set are 3.5 inches along each edg
- Understanding 81807
 The aquarium is 0.7m long and 25cm wide. The battery is deep if it can hold no more than 87.5 liters of water. I need help understanding how to calculate this.
The aquarium is 0.7m long and 25cm wide. The battery is deep if it can hold no more than 87.5 liters of water. I need help understanding how to calculate this. - Dimensions 81805
 The soap has the shape of a cuboid with dimensions of 6 cm, 4 cm, and 2 cm. Katy used it for a week and all the dimensions of the soap shrunk by half. How long will her soap last?
The soap has the shape of a cuboid with dimensions of 6 cm, 4 cm, and 2 cm. Katy used it for a week and all the dimensions of the soap shrunk by half. How long will her soap last? - Create 6
 Create a new drink can that will double the volume of the original can used. Dimensions of the can: 6cm diameter and 10cm height. You are to double the volume with the least amount of additional aluminum needed for the new can. There are 3 options : Optio
Create a new drink can that will double the volume of the original can used. Dimensions of the can: 6cm diameter and 10cm height. You are to double the volume with the least amount of additional aluminum needed for the new can. There are 3 options : Optio - Circumference of edges
 The hexagon pyramid has a circumference of 120 cm, and the length of the side edge is 25 cm. Calculate its volume.
The hexagon pyramid has a circumference of 120 cm, and the length of the side edge is 25 cm. Calculate its volume. - Cubes 81080
 How many cubes with an edge of 1 mm fit into a cube with an edge of 1 cm?
How many cubes with an edge of 1 mm fit into a cube with an edge of 1 cm?
- A piece 7
 A piece of dry ice is in the shape of a cube with edge lengths of 7cm. Find the surface area of the dry ice.
A piece of dry ice is in the shape of a cube with edge lengths of 7cm. Find the surface area of the dry ice. - The volume 7
 The volume of a cylindrical can is 75.36 in³. The diameter is 4 inches. Find the height. Use 3.14 as an estimation for pi.
The volume of a cylindrical can is 75.36 in³. The diameter is 4 inches. Find the height. Use 3.14 as an estimation for pi. - Calculate 78514
 The block has a length of 12 cm and a width of 0.6 dm. The height is the same size as the edge of a cube whose volume is 64cm³. Calculate the volume of the cuboid in cm³.
The block has a length of 12 cm and a width of 0.6 dm. The height is the same size as the edge of a cube whose volume is 64cm³. Calculate the volume of the cuboid in cm³.
