River
Calculate how many permille river Dunaj average falls, if on section long 957 km flowing water from 1454 m AMSL to 101 m AMSL.
Correct answer:

Tips for related online calculators
Need help calculating sum, simplifying, or multiplying fractions? Try our fraction calculator.
Our percentage calculator will help you quickly calculate various typical tasks with percentages.
Check out our ratio calculator.
Our permille calculator will help you quickly calculate various typical tasks with permilles.
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Our percentage calculator will help you quickly calculate various typical tasks with percentages.
Check out our ratio calculator.
Our permille calculator will help you quickly calculate various typical tasks with permilles.
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
- planimetrics
- right triangle
- triangle
- basic functions
- ratio
- percentages
- per mil
- numbers
- fractions
- rational numbers
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Quadrilateral 2
 Show that the quadrilateral with vertices P1(0,1), P2(4,2), P3(3,6) P4(-5,4) has two right triangles.
Show that the quadrilateral with vertices P1(0,1), P2(4,2), P3(3,6) P4(-5,4) has two right triangles. - Ratio of sides
 Calculate the area of a circle with the same circumference as the circumference of the rectangle inscribed with a circle with a radius of r 9 cm so that its sides are in a ratio of 2 to 7.
Calculate the area of a circle with the same circumference as the circumference of the rectangle inscribed with a circle with a radius of r 9 cm so that its sides are in a ratio of 2 to 7. - Annular area
 The square with side a = 1 is inscribed and circumscribed by circles. Find the annular area.
The square with side a = 1 is inscribed and circumscribed by circles. Find the annular area. - Quarter circle
 What is the radius of a circle inscribed in the quarter circle with a radius of 100 cm?
What is the radius of a circle inscribed in the quarter circle with a radius of 100 cm? - Cylinder horizontally
 The cylinder with a diameter of 3 m and a height/length of 15 m is laid horizontally. Water is poured into it, reaching a height of 60 cm below the cylinder's axis. How many hectoliters of water is in the cylinder?
The cylinder with a diameter of 3 m and a height/length of 15 m is laid horizontally. Water is poured into it, reaching a height of 60 cm below the cylinder's axis. How many hectoliters of water is in the cylinder? - Parallelogram 5027
 Calculate the area of the parallelogram if the side sizes are a = 80, b = 60, and the size of the diagonal angle is 60°.
Calculate the area of the parallelogram if the side sizes are a = 80, b = 60, and the size of the diagonal angle is 60°. - Circular segment
 Calculate the area S of the circular segment and the length of the circular arc l. The height of the circular segment is 2 cm, and the angle α = 60°. Help formula: S = 1/2 r². (Β-sinβ)
Calculate the area S of the circular segment and the length of the circular arc l. The height of the circular segment is 2 cm, and the angle α = 60°. Help formula: S = 1/2 r². (Β-sinβ) - Circular ring
 A square with an area of 16 centimeters is inscribed circle k1 and described to circle k2. Calculate the area of the circular ring, which circles k1, and k2 form.
A square with an area of 16 centimeters is inscribed circle k1 and described to circle k2. Calculate the area of the circular ring, which circles k1, and k2 form. - Circular pool
 The pool's base is a circle with a radius r = 10 m, excluding a circular segment that determines the chord length of 10 meters. The pool depth is h = 2m. How many hectoliters of water can fit into the pool?
The pool's base is a circle with a radius r = 10 m, excluding a circular segment that determines the chord length of 10 meters. The pool depth is h = 2m. How many hectoliters of water can fit into the pool? - Calculate triangle
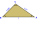 In the triangle, ABC, calculate the sizes of all heights, angles, perimeters, and area if given a=40cm, b=57cm, and c=59cm.
In the triangle, ABC, calculate the sizes of all heights, angles, perimeters, and area if given a=40cm, b=57cm, and c=59cm. - Angle of diagonals
 Calculate a rectangle's perimeter and area if its diagonal is 14 cm and the diagonals form an angle of 130°.
Calculate a rectangle's perimeter and area if its diagonal is 14 cm and the diagonals form an angle of 130°. - Maximum of volume
 The shell of the cone is formed by winding a circular section with a radius of 1. For what central angle of a given circular section will the volume of the resulting cone be maximum?
The shell of the cone is formed by winding a circular section with a radius of 1. For what central angle of a given circular section will the volume of the resulting cone be maximum? - Quadrilateral pyramid
 The height of a regular quadrilateral pyramid is 6.5 cm, and the angle between the base and the side wall is 42°. Calculate the surface area and volume of the body—round calculations to 1 decimal place.
The height of a regular quadrilateral pyramid is 6.5 cm, and the angle between the base and the side wall is 42°. Calculate the surface area and volume of the body—round calculations to 1 decimal place. - Quadrilateral oblique prism
 What is the volume of a quadrilateral oblique prism with base edges of length a = 1m, b = 1.1m, c = 1.2m, d = 0.7m if a side edge of length h = 3.9m has a deviation from the base of 20° 35' and the edges a, b form an angle of 50.5°?
What is the volume of a quadrilateral oblique prism with base edges of length a = 1m, b = 1.1m, c = 1.2m, d = 0.7m if a side edge of length h = 3.9m has a deviation from the base of 20° 35' and the edges a, b form an angle of 50.5°? - Flakes
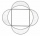 A circle was inscribed in the square. We draw a semicircle above each side of the square as above the diameter. This resulted in four chips. Which is bigger: the area of the middle square or the area of the four chips?
A circle was inscribed in the square. We draw a semicircle above each side of the square as above the diameter. This resulted in four chips. Which is bigger: the area of the middle square or the area of the four chips? - The trapezium
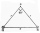 The trapezium is formed by cutting the top of the right-angled isosceles triangle. The trapezium base is 10 cm, and the top is 5 cm. Find the area of the trapezium.
The trapezium is formed by cutting the top of the right-angled isosceles triangle. The trapezium base is 10 cm, and the top is 5 cm. Find the area of the trapezium. - Company logo
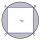 The company logo consists of a blue circle with a radius of 4 cm and an inscribed white square. What is the area of the blue part of the logo?
The company logo consists of a blue circle with a radius of 4 cm and an inscribed white square. What is the area of the blue part of the logo?
