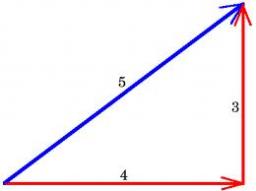
R triangle
Calculate the right triangle area whose longer leg is 6 dm shorter than the hypotenuse and 3 dm longer than the shorter leg.
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- quadratic equation
- inequalities
- equation
- system of equations
- planimetrics
- Pythagorean theorem
- right triangle
- triangle
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- A right 3
 A right triangle has a perimeter of 300 cm . its hypotenuse is 130cm. What are the lengths of the other sides .
A right triangle has a perimeter of 300 cm . its hypotenuse is 130cm. What are the lengths of the other sides . - Circle - analytics geometry
 Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0.
Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0. - Angles in a triangle
 In a triangle, the first angle measures a number plus 45°, and the second angle is 30° less than the first angle. The third angle is two times the number more than the first angle. What are the measurements of each angle of the triangle?
In a triangle, the first angle measures a number plus 45°, and the second angle is 30° less than the first angle. The third angle is two times the number more than the first angle. What are the measurements of each angle of the triangle? - 11990 perimeter RT
 A right triangle has integer side lengths and a perimeter of 11990. In addition, we know that one of its perpendiculars has a prime number length. Find its length.
A right triangle has integer side lengths and a perimeter of 11990. In addition, we know that one of its perpendiculars has a prime number length. Find its length.
- One leg
 One leg of a right triangle is 1 foot longer than the other leg. The hypotenuse is 5 feet. Find the lengths of the three sides of the triangle.
One leg of a right triangle is 1 foot longer than the other leg. The hypotenuse is 5 feet. Find the lengths of the three sides of the triangle. - The sides
 The sides of a right triangle form an arithmetic sequence. The hypotenuse is 24 cm long. Determine the remaining sides of the triangle.
The sides of a right triangle form an arithmetic sequence. The hypotenuse is 24 cm long. Determine the remaining sides of the triangle. - Outside point
 The square ABCD and the point E lying outside the given square are given. What is the area of the square when the distance | AE | = 2, | DE | = 5 a | BE | = 4?
The square ABCD and the point E lying outside the given square are given. What is the area of the square when the distance | AE | = 2, | DE | = 5 a | BE | = 4? - Arm and base
 The isosceles triangle has a circumference of 46 cm. If the arm is 5 cm longer than the base, calculate its area.
The isosceles triangle has a circumference of 46 cm. If the arm is 5 cm longer than the base, calculate its area. - Railway embankment
 The railway embankment section is an isosceles trapezoid, and the bases' sizes are in the ratio of 5:3. The arms have a length of 5 m, and the embankment height is 4.8 m. Calculates the size of the embankment section area.
The railway embankment section is an isosceles trapezoid, and the bases' sizes are in the ratio of 5:3. The arms have a length of 5 m, and the embankment height is 4.8 m. Calculates the size of the embankment section area.
- Isosceles triangle
 In an isosceles triangle ABC with base AB; A [3,4]; B [1,6] and the vertex C lies on the line 5x - 6y - 16 = 0. Calculate the coordinates of vertex C.
In an isosceles triangle ABC with base AB; A [3,4]; B [1,6] and the vertex C lies on the line 5x - 6y - 16 = 0. Calculate the coordinates of vertex C. - Equation of the circle
 Find the equation of the circle inscribed in the rhombus ABCD where A[1, -2], B[8, -3], and C[9, 4].
Find the equation of the circle inscribed in the rhombus ABCD where A[1, -2], B[8, -3], and C[9, 4]. - The tower
 The observer sees the tower's base 96 meters high at a depth of 30 degrees and 10 minutes and the top of the tower at a depth of 20 degrees and 50 minutes. How high is the observer above the horizontal plane on which the tower stands?
The observer sees the tower's base 96 meters high at a depth of 30 degrees and 10 minutes and the top of the tower at a depth of 20 degrees and 50 minutes. How high is the observer above the horizontal plane on which the tower stands? - An equilateral
 An equilateral triangle is inscribed in a square of side 1 unit long so that it has one common vertex with the square. What is the area of the inscribed triangle?
An equilateral triangle is inscribed in a square of side 1 unit long so that it has one common vertex with the square. What is the area of the inscribed triangle? - Three parallels
 The vertices of an equilateral triangle lie on three different parallel lines. The middle line is 5 m and 3 m distant from the end lines. Calculate the height of this triangle.
The vertices of an equilateral triangle lie on three different parallel lines. The middle line is 5 m and 3 m distant from the end lines. Calculate the height of this triangle.
- Sides of right angled triangle
 One leg is 1 m shorter than the hypotenuse, and the second leg is 2 m shorter than the hypotenuse. Find the lengths of all sides of the right-angled triangle.
One leg is 1 m shorter than the hypotenuse, and the second leg is 2 m shorter than the hypotenuse. Find the lengths of all sides of the right-angled triangle. - Faces diagonals
 If a cuboid's diagonals are x, y, and z (wall diagonals or three faces), find the cuboid volume. Solve for x=1.3, y=1, z=1.2
If a cuboid's diagonals are x, y, and z (wall diagonals or three faces), find the cuboid volume. Solve for x=1.3, y=1, z=1.2 - Two chords
 Calculate the length of chord AB and perpendicular chord BC to the circle if AB is 4 cm from the circle's center and BC 8 cm from the center.
Calculate the length of chord AB and perpendicular chord BC to the circle if AB is 4 cm from the circle's center and BC 8 cm from the center.
