Cuboids
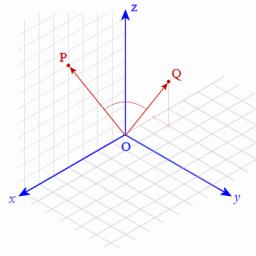
Two separate cuboids with different orientations are in space. Determine the angle between them, knowing the direction cosine matrix for each separate cuboid. u1=(0.62955056, 0.094432584, 0.77119944) u2=(0.14484653, 0.9208101, 0.36211633)
Correct answer:
Showing 1 comment:
Matikar
use scalar products to determine angle between two 3D vectors (if direction cosines gives -> its unit vectors)
Tips for related online calculators
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Matrices 2
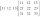 Suppose A=(1 6 3 −2) B=(4 −3 −4 3) find 2A+3B
Suppose A=(1 6 3 −2) B=(4 −3 −4 3) find 2A+3B - Elimination: 10441
 Solve the linear system of equations by Gaussian elimination: 3x1 −2x2 −5x3 + x4 = 3 2x1 −3x2 + x3 + 5x4 = −3 x1 + 2x2 −4x4 = −3 x1 - x2 −4x3 + 9x4 = 22
Solve the linear system of equations by Gaussian elimination: 3x1 −2x2 −5x3 + x4 = 3 2x1 −3x2 + x3 + 5x4 = −3 x1 + 2x2 −4x4 = −3 x1 - x2 −4x3 + 9x4 = 22 - Inverse matrix
 Find out the inverse by Gauss elimination or by reduction method. A=[2/3. 1 -3. 1/3]
Find out the inverse by Gauss elimination or by reduction method. A=[2/3. 1 -3. 1/3] - The determinant
 The determinant of the unit matrix equals 7. Check how many rows the A matrix contains.
The determinant of the unit matrix equals 7. Check how many rows the A matrix contains. - Inverse matrix
 Find how many times the larger determinant is the matrix A, which equals 9 as the determinant of its inverse matrix.
Find how many times the larger determinant is the matrix A, which equals 9 as the determinant of its inverse matrix. - The inverse
 The inverse matrix for matrix A has a determinant value of 0.333. What value has a determinant of matrix A?
The inverse matrix for matrix A has a determinant value of 0.333. What value has a determinant of matrix A?
