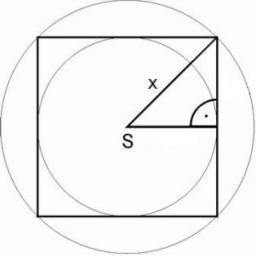
Square and circles
Square with sides 83 cm is circumscribed and inscribed with circles. Determine the radiuses of both circles.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Perfect square or cube
 Would you classify 324 as a perfect square, perfect cube, both, or neither? ...
Would you classify 324 as a perfect square, perfect cube, both, or neither? ... - A frustum
 A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume.
A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume. - Colour
 The square is divided into 100 squares. If you needed to color 49%, how many squares would you color?
The square is divided into 100 squares. If you needed to color 49%, how many squares would you color? - Perimeter 81600
 The radius of the circular bed is 2 m. Around it is an area filled with sand, the border of which is formed by the sides of a square with a length of 5 m and the bed's perimeter. Calculate the volume of the area covered with sand.
The radius of the circular bed is 2 m. Around it is an area filled with sand, the border of which is formed by the sides of a square with a length of 5 m and the bed's perimeter. Calculate the volume of the area covered with sand. - Quadrilateral calc
 The square ABCD is given. The midpoint of AB is E, the midpoint of BC is F, CD is G, and the midpoint of DA is H. Join AF, BG, CH, and DE. Inside the square (approximately in the middle), the intersections of these line segments form a quadrilateral. Calc
The square ABCD is given. The midpoint of AB is E, the midpoint of BC is F, CD is G, and the midpoint of DA is H. Join AF, BG, CH, and DE. Inside the square (approximately in the middle), the intersections of these line segments form a quadrilateral. Calc - A cone 3
 A cone has a diameter of x cm and a slant height of y cm. A square pyramid has a base side length of x cm and a slant height of y cm. Which has the greater surface area? Explain.
A cone has a diameter of x cm and a slant height of y cm. A square pyramid has a base side length of x cm and a slant height of y cm. Which has the greater surface area? Explain. - A square 4
 A square plot of land has an area of 20.25 ha. The owner fenced it with Three strands of wire. What length of wire did he use for the whole plot?
A square plot of land has an area of 20.25 ha. The owner fenced it with Three strands of wire. What length of wire did he use for the whole plot? - The perimeter
 The perimeter of the base of a regular quadrilateral pyramid is the same as its height. The pyramid has a volume of 288 dm³. Calculate its surface area round the result to the whole dm².
The perimeter of the base of a regular quadrilateral pyramid is the same as its height. The pyramid has a volume of 288 dm³. Calculate its surface area round the result to the whole dm². - Square room 2
 A square room has a floor area of 144 square feet. The height of the room is 6 feet. What is the area of one wall?
A square room has a floor area of 144 square feet. The height of the room is 6 feet. What is the area of one wall? - Three 205
 Three metallic bars of lengths 400 cm, 600 cm, and 720 cm are cut into equal pieces. Find the largest possible area of a square that can be made from any of the three bars.
Three metallic bars of lengths 400 cm, 600 cm, and 720 cm are cut into equal pieces. Find the largest possible area of a square that can be made from any of the three bars. - Figure
 Figure A is a scale image of Figure B, as shown. (figure a is 6 inches, and figure b is x inches, both squares) The scale that maps Figure A onto Figure B is 1:1 1/3. Enter the value f x
Figure A is a scale image of Figure B, as shown. (figure a is 6 inches, and figure b is x inches, both squares) The scale that maps Figure A onto Figure B is 1:1 1/3. Enter the value f x - A farmer 6
 A farmer made a square chicken coop of 6 1/3m. Determine the perimeter of the chicken coop. (Recall: perimeter =add all sides)
A farmer made a square chicken coop of 6 1/3m. Determine the perimeter of the chicken coop. (Recall: perimeter =add all sides) - Square field
 The perimeter of a square field is 64 m. Find the cost of cementing the field at the cost of 240 USD per square meter.
The perimeter of a square field is 64 m. Find the cost of cementing the field at the cost of 240 USD per square meter. - In an
 In an ABCD square, n interior points are chosen on each side. Find the number of all triangles whose vertices X, Y, and Z lie at these points and on different sides of the square.
In an ABCD square, n interior points are chosen on each side. Find the number of all triangles whose vertices X, Y, and Z lie at these points and on different sides of the square. - Rafael
 Rafael has three squares. The first square has a side length of 2 cm. The second square has a side length of 4 cm, and its vertex is placed in the center of the first square. The last square has a side length of 6 cm, and its vertex is placed in the cente
Rafael has three squares. The first square has a side length of 2 cm. The second square has a side length of 4 cm, and its vertex is placed in the center of the first square. The last square has a side length of 6 cm, and its vertex is placed in the cente - Isosceles right triangle
 If the square of the hypotenuse of an isosceles right triangle is 128 cm2, find the length of each side.
If the square of the hypotenuse of an isosceles right triangle is 128 cm2, find the length of each side. - Circumference 72984
 Task 1 - The circumference of the square is 280 mm. What is its area? Task 2 - the perimeter of the rectangle is 44.6dm, and its width is 6.3dm. Calculate the area of this rectangle.
Task 1 - The circumference of the square is 280 mm. What is its area? Task 2 - the perimeter of the rectangle is 44.6dm, and its width is 6.3dm. Calculate the area of this rectangle.
