Hexagon cut pyramid
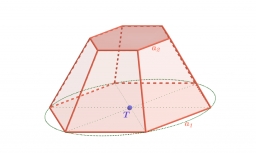
Calculate the volume of a regular 6-sided cut pyramid if the bottom edge is 30 cm, the top edge is 12 cm, and the side edge length is 41 cm.
Correct answer:
Tips for related online calculators
See also our right triangle calculator.
Do you want to convert length units?
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
Do you want to convert length units?
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- geometry
- similarity of triangles
- algebra
- expression of a variable from the formula
- arithmetic
- square root
- solid geometry
- similarity bodies
- pyramid
- frustum
- planimetrics
- Pythagorean theorem
- right triangle
- polygon
- area of a shape
- triangle
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Square grid
 A square grid consists of a square with sides of a length of 1 cm. Draw at least three patterns, each with an area of 6 cm² and a circumference of 12 cm, and their sides in a square grid.
A square grid consists of a square with sides of a length of 1 cm. Draw at least three patterns, each with an area of 6 cm² and a circumference of 12 cm, and their sides in a square grid. - Rings groups
 Twenty-seven pupils attend some groups. Fourteen pupils attend the Dance group, 21 sports group, and 16 in the dramatic group. Dance and sporting attend nine pupils, dance and drama six pupils, sporty and dramatic 11 pupils. How many pupils attend all thr
Twenty-seven pupils attend some groups. Fourteen pupils attend the Dance group, 21 sports group, and 16 in the dramatic group. Dance and sporting attend nine pupils, dance and drama six pupils, sporty and dramatic 11 pupils. How many pupils attend all thr - Cents
 Julka has 3 cents more than Hugo. Together, they have 27 cents. How many cents has Julka and how many Hugo?
Julka has 3 cents more than Hugo. Together, they have 27 cents. How many cents has Julka and how many Hugo? - Store
 Peter paid 3 euros in store, more than half the amount on arrival at the store. When he left the shop, he remains 10 euros. How many euros does he have upon arrival at the store?
Peter paid 3 euros in store, more than half the amount on arrival at the store. When he left the shop, he remains 10 euros. How many euros does he have upon arrival at the store?
- Lentilka
 Lentilka made 31 pancakes. Eight don't fill with anything, 14 pancakes filled with strawberry jam, and 16 filled with cream cheese. a) How many Lentilka did strawberry-cream cheese pancakes? Maksik ate four strawberry-cream cheese and all pure strawberry
Lentilka made 31 pancakes. Eight don't fill with anything, 14 pancakes filled with strawberry jam, and 16 filled with cream cheese. a) How many Lentilka did strawberry-cream cheese pancakes? Maksik ate four strawberry-cream cheese and all pure strawberry - Rabbits
 In the hutch are 48 mottled rabbits. Brown is 23 less than mottled, and white is 8 times less than mottled. How many rabbits are in the hutch?
In the hutch are 48 mottled rabbits. Brown is 23 less than mottled, and white is 8 times less than mottled. How many rabbits are in the hutch? - Segments
 Line segments 69 cm and 3.7 dm long we divide into equal parts which lengths in centimeters is expressed integer. How many ways can we divide?
Line segments 69 cm and 3.7 dm long we divide into equal parts which lengths in centimeters is expressed integer. How many ways can we divide? - Ravens
 The tale of the Seven Ravens was seven brothers, each of whom was born exactly 2.5 years after the previous one when the eldest of the brothers was 2-times older than the youngest, mother all curse. How old were seven ravens brothers when their mother cur
The tale of the Seven Ravens was seven brothers, each of whom was born exactly 2.5 years after the previous one when the eldest of the brothers was 2-times older than the youngest, mother all curse. How old were seven ravens brothers when their mother cur - Numbers
 Determine the number of all positive integers less than 4183444 if each is divisible by 29, 7, 17. What is its sum?
Determine the number of all positive integers less than 4183444 if each is divisible by 29, 7, 17. What is its sum?
- Gear
 Two gears fit into each other and have a transfer of 2:3. Centers of gears are spaced 82 cm. What are the radii of the gears?
Two gears fit into each other and have a transfer of 2:3. Centers of gears are spaced 82 cm. What are the radii of the gears? - Monkey
 The monkey fell into 20 meters deep well. Every day it climbs 3 meters, at night it drops back by 2 m. On what day it gets out from the well?
The monkey fell into 20 meters deep well. Every day it climbs 3 meters, at night it drops back by 2 m. On what day it gets out from the well? - A cone 3
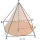 A cone has a diameter of x cm and a slant height of y cm. A square pyramid has a base side length of x cm and a slant height of y cm. Which has the greater surface area? Explain.
A cone has a diameter of x cm and a slant height of y cm. A square pyramid has a base side length of x cm and a slant height of y cm. Which has the greater surface area? Explain. - Clubhouse
 There were only chairs and tables in the clubhouse. Each chair had four legs, and the table was triple. Scouts came to the clubhouse. Everyone sat on their chair, two chairs were left unoccupied, and the number of legs in the room was 101. How many chairs
There were only chairs and tables in the clubhouse. Each chair had four legs, and the table was triple. Scouts came to the clubhouse. Everyone sat on their chair, two chairs were left unoccupied, and the number of legs in the room was 101. How many chairs - Two rectangles
 I cut out two rectangles with 54 cm² and 90 cm². Their sides are expressed in whole centimeters. If I put these rectangles together, I get a rectangle with an area of 144 cm². What dimensions can this large rectangle have? Write all options. Explain your
I cut out two rectangles with 54 cm² and 90 cm². Their sides are expressed in whole centimeters. If I put these rectangles together, I get a rectangle with an area of 144 cm². What dimensions can this large rectangle have? Write all options. Explain your
- Inscription 4864
 From the beginning of the year, students in 4th grade wrote a chronicle. She had everything they had together, and they cared a lot about her. But one day, the chronicle was lost. Five students were left to search for everything on Monday after the class.
From the beginning of the year, students in 4th grade wrote a chronicle. She had everything they had together, and they cared a lot about her. But one day, the chronicle was lost. Five students were left to search for everything on Monday after the class. - Seagull
 An artificially created island in the shape of a circle with a radius of 50 m is overgrown with grass. The only exception is a landing area for helicopters in the shape of a rectangle measuring 15 m and 8 m. What is the probability that the flying seagull
An artificially created island in the shape of a circle with a radius of 50 m is overgrown with grass. The only exception is a landing area for helicopters in the shape of a rectangle measuring 15 m and 8 m. What is the probability that the flying seagull - Goat, cabbage and wolf
 A man once had to travel with a wolf, a goat, and a cabbage. He had to take good care of them since the wolf would like to taste a.piece of goat if he got the chance, while the goat appeared too long for a tasty cabbage. After some traveling, he suddenly
A man once had to travel with a wolf, a goat, and a cabbage. He had to take good care of them since the wolf would like to taste a.piece of goat if he got the chance, while the goat appeared too long for a tasty cabbage. After some traveling, he suddenly
