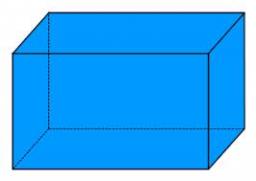
Cuboid
Cuboid with edge a=6 cm and space diagonal u=31 cm has volume V=900 cm3. Calculate the length of the other edges.
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a system of equations and looking for calculator system of linear equations?
Do you want to convert length units?
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Do you have a system of equations and looking for calculator system of linear equations?
Do you want to convert length units?
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- quadratic equation
- system of equations
- biquadratic equation
- arithmetic
- square root
- square (second power, quadratic)
- solid geometry
- cuboid
- space diagonal
- planimetrics
- Pythagorean theorem
- right triangle
- triangle
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- The factory 3
 The factory is 18 km away from the city. A cyclist leaves the factory for the city, and half an hour after him from the same place, a motorcyclist arrives 6 minutes before the cyclist in the city. Find the speed of each, knowing that the speed of the cycl
The factory is 18 km away from the city. A cyclist leaves the factory for the city, and half an hour after him from the same place, a motorcyclist arrives 6 minutes before the cyclist in the city. Find the speed of each, knowing that the speed of the cycl - Mountain climbing
 Ken and his brother decided to go on mountain climbing 8 miles from their house to Mt. Daraitan at a rate of x mph (miles per hour). For the return trip, it was 2 mph faster. It took them 6 hours for the entire round trip. What is the x?
Ken and his brother decided to go on mountain climbing 8 miles from their house to Mt. Daraitan at a rate of x mph (miles per hour). For the return trip, it was 2 mph faster. It took them 6 hours for the entire round trip. What is the x? - The length 11
 The length of a rectangle is four times its width. If the area is 100 m², what is the length of the rectangle?
The length of a rectangle is four times its width. If the area is 100 m², what is the length of the rectangle? - Book Store
 The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w
The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w
- A missile
 A missile is fired with a speed of 100 fps in a direction 30° above the horizontal. Determine the maximum height to which it rises. Fps foot per second.
A missile is fired with a speed of 100 fps in a direction 30° above the horizontal. Determine the maximum height to which it rises. Fps foot per second. - A Cartesian framework
 1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap
1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap - Staircase
 On a staircase 3.6 meters high, the number of steps would increase by three if the height of one step decreased by 4 cm. How high are the stairs?
On a staircase 3.6 meters high, the number of steps would increase by three if the height of one step decreased by 4 cm. How high are the stairs? - Isosceles triangle
 In an isosceles triangle ABC with base AB; A [3,4]; B [1,6] and the vertex C lies on the line 5x - 6y - 16 = 0. Calculate the coordinates of vertex C.
In an isosceles triangle ABC with base AB; A [3,4]; B [1,6] and the vertex C lies on the line 5x - 6y - 16 = 0. Calculate the coordinates of vertex C. - Lookout tower
 How high is the lookout tower? If each step was 3 cm lower, 60 more were on the lookout tower. If it were 3 cm higher again, it would be 40 less than it is now.
How high is the lookout tower? If each step was 3 cm lower, 60 more were on the lookout tower. If it were 3 cm higher again, it would be 40 less than it is now.
- Circle and square
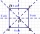 An ABCD square with a side length of 100 mm is given. Calculate the circle’s radius that passes through vertices B, C, and the center of the side AD.
An ABCD square with a side length of 100 mm is given. Calculate the circle’s radius that passes through vertices B, C, and the center of the side AD. - A map
 A map with a scale of 1:5,000 shows a rectangular field with an area of 18 ha. The length of the field is three times its width. The area of the field on the map is 72 cm square. What is the actual length and width of the field?
A map with a scale of 1:5,000 shows a rectangular field with an area of 18 ha. The length of the field is three times its width. The area of the field on the map is 72 cm square. What is the actual length and width of the field? - Difference of legs
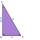 In a right triangle, the hypotenuse length is 65 m, and the difference between legs is 23 m. Calculate the perimeter of this triangle.
In a right triangle, the hypotenuse length is 65 m, and the difference between legs is 23 m. Calculate the perimeter of this triangle. - Suppose
 Suppose you know that the length of a line segment is 15, x2=6, y2=14, and x1= -3. Find the possible value of y1. Is there more than one possible answer? Why or why not?
Suppose you know that the length of a line segment is 15, x2=6, y2=14, and x1= -3. Find the possible value of y1. Is there more than one possible answer? Why or why not? - Rectangle field
 The field has a shape of a rectangle, having a length of 119 m and a width of 19 m. , How many meters have to shorten its length and increase its width to maintain its area and circumference increased by 24 m?
The field has a shape of a rectangle, having a length of 119 m and a width of 19 m. , How many meters have to shorten its length and increase its width to maintain its area and circumference increased by 24 m?
- Three parallels
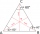 The vertices of an equilateral triangle lie on three different parallel lines. The middle line is 5 m and 3 m distant from the end lines. Calculate the height of this triangle.
The vertices of an equilateral triangle lie on three different parallel lines. The middle line is 5 m and 3 m distant from the end lines. Calculate the height of this triangle. - Two chords
 Calculate the length of chord AB and perpendicular chord BC to the circle if AB is 4 cm from the circle's center and BC 8 cm from the center.
Calculate the length of chord AB and perpendicular chord BC to the circle if AB is 4 cm from the circle's center and BC 8 cm from the center. - Two cyclists 2
 At the same time, two cyclists left towns A and B at constant speeds. The first one goes from town A to town B, and the second one from town B to town A. At one point during the trip, they met. After they met, the first cyclist arrived at town B in 36min,
At the same time, two cyclists left towns A and B at constant speeds. The first one goes from town A to town B, and the second one from town B to town A. At one point during the trip, they met. After they met, the first cyclist arrived at town B in 36min,
