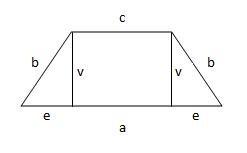
Isosceles trapezoid
Calculate the area of an isosceles trapezoid whose bases are at a ratio of 5:3. The arm is 6cm long and 4cm high.
Correct answer:
Tips for related online calculators
Check out our ratio calculator.
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Length 26
 The length of the median of the trapezoid is 10 inches. The median divides the trapezoid into two areas whose ratio is 3:5. The length of the shorter base is:
The length of the median of the trapezoid is 10 inches. The median divides the trapezoid into two areas whose ratio is 3:5. The length of the shorter base is: - Similar frustums
 The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums?
The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums? - Pentagon
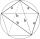 The signboard has the shape of a pentagon ABCDE, in which line BC is perpendicular to line AB, and EA is perpendicular to line AB. Point P is the heel of the vertical starting from point D on line AB. | AP | = | PB |, | BC | = | EA | = 6dm, | PD | = 8.4dm
The signboard has the shape of a pentagon ABCDE, in which line BC is perpendicular to line AB, and EA is perpendicular to line AB. Point P is the heel of the vertical starting from point D on line AB. | AP | = | PB |, | BC | = | EA | = 6dm, | PD | = 8.4dm - What is
 What is the circumference of an isosceles trapezoid with an area of 106.75 cm²? The lengths of the sides are in the ratio of 1:3:2:1, and the bases are 6.1 cm apart.
What is the circumference of an isosceles trapezoid with an area of 106.75 cm²? The lengths of the sides are in the ratio of 1:3:2:1, and the bases are 6.1 cm apart.
- Ratio in trapezium
 The height v and the base a, c in the trapezoid ABCD is in the ratio 1:6:3, its area S = 324 square cm. Peak angle B = 35 degrees. Determine the perimeter of the trapezoid
The height v and the base a, c in the trapezoid ABCD is in the ratio 1:6:3, its area S = 324 square cm. Peak angle B = 35 degrees. Determine the perimeter of the trapezoid - Railway embankment
 The railway embankment section is an isosceles trapezoid, and the bases' sizes are in the ratio of 5:3. The arms have a length of 5 m, and the embankment height is 4.8 m. Calculates the size of the embankment section area.
The railway embankment section is an isosceles trapezoid, and the bases' sizes are in the ratio of 5:3. The arms have a length of 5 m, and the embankment height is 4.8 m. Calculates the size of the embankment section area. - Garden exchange
 The garden has a rectangular trapezoid shape, the bases of which have dimensions of 60 m and 30 m and a vertical arm of 40 m. The owner exchanged this garden for a parallelogram, which is 7/9 of the area of a trapezoidal garden. What is the size of the ne
The garden has a rectangular trapezoid shape, the bases of which have dimensions of 60 m and 30 m and a vertical arm of 40 m. The owner exchanged this garden for a parallelogram, which is 7/9 of the area of a trapezoidal garden. What is the size of the ne - Diagonal intersect
 Isosceles trapezoid ABCD with length bases | AB | = 6 cm, CD | = 4 cm is divided into four triangles by the diagonals intersecting at point S. How much of the area of the trapezoid are ABS and CDS triangles?
Isosceles trapezoid ABCD with length bases | AB | = 6 cm, CD | = 4 cm is divided into four triangles by the diagonals intersecting at point S. How much of the area of the trapezoid are ABS and CDS triangles? - There
 There is a stretched steel cable between the three columns. The height of the first column is 4 m, and the height of the second is 3.5 m. The distance between the first two columns is 2.5 m, and the distance between the second and third is 5 m. The heels
There is a stretched steel cable between the three columns. The height of the first column is 4 m, and the height of the second is 3.5 m. The distance between the first two columns is 2.5 m, and the distance between the second and third is 5 m. The heels
- Trapezium diagonals
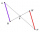 It is given trapezium ABCD with bases | AB | = 12 cm, |CD| = 8 cm. Point S is the intersection of the diagonals for which |AS| is 6 cm long. Calculate the length of the full diagonal AC.
It is given trapezium ABCD with bases | AB | = 12 cm, |CD| = 8 cm. Point S is the intersection of the diagonals for which |AS| is 6 cm long. Calculate the length of the full diagonal AC. - Trapezoid - intersection of diagonals
 In the ABCD trapezoid is AB = 8 cm long, trapezium height 6 cm, and distance of diagonals intersection from AB is 4 cm. Calculate the trapezoid area.
In the ABCD trapezoid is AB = 8 cm long, trapezium height 6 cm, and distance of diagonals intersection from AB is 4 cm. Calculate the trapezoid area. - MO Z9–I–2 - 2017
 VO is a longer base in the VODY trapezoid, and the diagonal intersection K divides the VD line in a 3:2 ratio. The area of the KOV triangle is 13.5 cm². Find the area of the entire trapezoid.
VO is a longer base in the VODY trapezoid, and the diagonal intersection K divides the VD line in a 3:2 ratio. The area of the KOV triangle is 13.5 cm². Find the area of the entire trapezoid. - Trapezoid - central median
 The central median divides the trapezoid into two smaller trapezoids. Find the ratio of its areas.
The central median divides the trapezoid into two smaller trapezoids. Find the ratio of its areas. - Isosceles trapezoid
 In an isosceles trapezoid KLMN, the intersection of the diagonals is marked by the letter S. Calculate the area of the trapezoid if /KS/: /SM/ = 2:1 and a triangle KSN is 14 cm².
In an isosceles trapezoid KLMN, the intersection of the diagonals is marked by the letter S. Calculate the area of the trapezoid if /KS/: /SM/ = 2:1 and a triangle KSN is 14 cm².
- Trapezium
 The length of the base and the height size of the trapezium base are at a ratio of 5:3:2. The area of the trapezium is 128 cm². Calculate the length of the base and the height of the trapezoid.
The length of the base and the height size of the trapezium base are at a ratio of 5:3:2. The area of the trapezium is 128 cm². Calculate the length of the base and the height of the trapezoid. - Trapezoid
 Area of trapezoid is 135 cm². Sides a, c and height h are in a ratio of 6:4:3. How long are a,c and h? Make calculation.
Area of trapezoid is 135 cm². Sides a, c and height h are in a ratio of 6:4:3. How long are a,c and h? Make calculation. - Trapezoid RT
 The plot has a shape of a rectangular trapezium ABCD, where ABIICD with a right angle at the vertex B. side AB has a length of 36 m. The lengths of the sides AB and BC are in the ratio 12:7. Lengths of the sides AB and CD are a ratio of 3:2. Calculate con
The plot has a shape of a rectangular trapezium ABCD, where ABIICD with a right angle at the vertex B. side AB has a length of 36 m. The lengths of the sides AB and BC are in the ratio 12:7. Lengths of the sides AB and CD are a ratio of 3:2. Calculate con
